题目内容
16.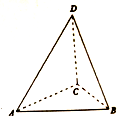 如图,在三棱锥D-ABC中,$AC=BC=1,CD=AB=\sqrt{2},AD=BD=\sqrt{3}$,若该三棱锥的四个顶点均在同一球面上,则该球的体积为( )
如图,在三棱锥D-ABC中,$AC=BC=1,CD=AB=\sqrt{2},AD=BD=\sqrt{3}$,若该三棱锥的四个顶点均在同一球面上,则该球的体积为( )| A. | $\frac{32π}{3}$ | B. | 4π | C. | 2π | D. | $\frac{4π}{3}$ |
分析 利用已知条件说明三棱锥是长方体的一个角,扩展几何体为长方体,求出外接球的半径,然后求解球的体积.
解答 解:在三棱锥D-ABC中,$AC=BC=1,CD=AB=\sqrt{2},AD=BD=\sqrt{3}$,
可得AC⊥BC,AC⊥CD,CD⊥CB,则C-ABD三棱锥看作是长方体的一个角,三棱锥的外接球计算长方体的外接球,
外接球的半径为:$\frac{1}{2}\sqrt{1+2+1}$=1.
外接球的体积为:$\frac{4π}{3}×{1}^{3}$=$\frac{4π}{3}$.
故选:D.
点评 本题考查三棱锥的外接球的体积的求法,考查空间想象能力以及最后思想计算能力.

练习册系列答案
相关题目
11.已知f(x)=x2+3x,若|x-a|≤1,则下列不等式一定成立的是( )
| A. | |f(x)-f(a)|≤3|a|+3 | B. | |f(x)-f(a)|≤2|a|+4 | C. | |f(x)-f(a)|≤|a|+5 | D. | |f(x)-f(a)|≤2(|a|+1)2 |
1.已知棱长为2,各面均为等边三角形的四面体S-ABC的各顶点都在球O的球面上,则球O的表面积为( )
| A. | π | B. | 2π | C. | 4π | D. | 6π |