题目内容
15.已知不等式x2-3x<0的解集是A,不等式x2+x-6<0的解集是B,不等式x2+ax+b<0的解集是A∩B,那么a=( )| A. | -2 | B. | 1 | C. | -1 | D. | 2 |
分析 利用一元二次不等式的解法和根与系数的关系,即可得出结论.
解答 解:解不等式x2-3x<0,得A={x|0<x<3},
解不等式x2+x-6<0,得B={x|-3<x<2},
又不等式x2+ax+b<0的解集是A∩B={x|0<x<2},
由根与系数的关系得-a=0+2,解得a=-2.
故选:A.
点评 熟练掌握一元二次不等式的解法以及“三个二次”之间的关系是解题的关键.

练习册系列答案
相关题目
3.某程序框图如图所示,若输入的n=10,则输出结果为( )
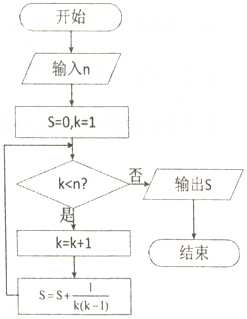

| A. | $\frac{1}{10}$ | B. | $\frac{8}{9}$ | C. | $\frac{9}{10}$ | D. | $\frac{10}{11}$ |
3.已知a=($\frac{3}{5}$)${\;}^{-\frac{1}{3}}$,b=($\frac{5}{3}$)${\;}^{\frac{1}{4}}$,c=($\frac{3}{2}$)${\;}^{-\frac{3}{4}}$,则a,b,c的大小关系是( )
| A. | c<a<b | B. | a<b<c | C. | b<a<c | D. | c<b<a |
10.椭圆的中心在坐标原点,焦点在x轴上,左右顶点分别为A1、A2,上下顶点分别为B1、B2,F2为右焦点,延长B2F2与A2B1交于点P,若∠B2PA2为钝角,则该椭圆离心率的取值范围是( )
| A. | $({\frac{{\sqrt{5}-2}}{2},0})$ | B. | $({0,\frac{{\sqrt{5}-2}}{2}})$ | C. | $({0,\frac{{\sqrt{5}-1}}{2}})$ | D. | $({\frac{{\sqrt{5}-1}}{2},1})$ |
7.某产品的广告费用x与销售额y的统计数据如表:
根据上表可得回归方程y=bx+a中的b为9.4,据此模型预报广告费用为6万元时销售额为( )
| 广告费用x(万元) | 8 | 3 | 4 | 5 |
| 销售额y(万元) | 54 | 26 | 39 | 41 |
| A. | 47.4 万元 | B. | 57.7万元 | C. | 49.4万元 | D. | 62.4万元 |