题目内容
“函数f（x）=x2+2x+m存在零点”的一个必要不充分条件是（ ）
| A、m≤1 | B、m≤2 |
| C、m≤0 | D、1≤m≤2 |
考点：必要条件、充分条件与充要条件的判断
专题：函数的性质及应用
分析：根据函数存在零点的等价条件求出对应的充要条件，根据充分条件和必要条件的定义进行判断即可得到结论．
解答：
解：若函数f（x）=x2+2x+m存在零点，则对应的判别式△=4-4m≥0，
解得m≤1，
则m≤2是m≤1的一个必要不充分条件，
故选：B．
解得m≤1，
则m≤2是m≤1的一个必要不充分条件，
故选：B．
点评：本题主要考查充分条件和必要条件的判断，利用函数存在零点的等价条件是解决本题的关键．比较基础．
练习册系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
已知中心在原点、焦点在x轴上的椭圆C1与双曲线C2有共同的焦点，设左右焦点分别为F1，F2，P是C1与C2在第一象限的交点，△PF1F2是以PF1为底边的等腰三角形，若椭圆与双曲线的离心率分别为e1，e2，则e1•e2的取值范围是（ ）
A、（
| ||
B、（
| ||
C、（
| ||
| D、（0，+∞） |
有红、蓝、黄、绿四种颜色的球各6个，每种颜色的6个球分别标有数字1、2、3、4、5、6，从中任取3个标号不同的球，这3个颜色互不相同且所标数字互不相邻的取法种数为（ ）
| A、80 | B、84 | C、96 | D、104 |
设a＞0，b＞0，c＞0下列不等关系不恒成立的是（ ）
A、c3+c+1＞c2+
| ||||
| B、|a-b|≤|a-c|+|b-c| | ||||
C、若a+4b=1，则
| ||||
| D、ax2+bx+c≥0（x∈R） |
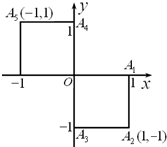甲、乙、丙三人中要选一人去参加唱歌比赛，于是他们制定了一个规则，规则为：（如图）以O为起点，再从A1，A2，A3，A4，A5，这5个点中任取两点分别为终点得到两个向量，记这两个向量的数量积为X，若X＞0就让甲去；若X=0就让乙去；若X＜0就是丙去．