题目内容
设定义在[x1,x2]的函数y=f(x)的图象的两个端点为A(x1,y1),B(x2,y2).M(x,y)是f(x)图象上任意一点,其中x=λx1+(1-λ)x2,(λ∈R),且
=λ
+(1-λ)
,若不等式|
|≤k恒成立,则称函数f(x)在[x1,x2]上“k阶线性近似”.若函数y=
与y=
在[0,1]上有且仅有一个“k阶线性近似”,则实数k的取值范围为 .
| ON |
| OA |
| OB |
| MN |
| x |
| 3 | x |
考点:幂函数的性质
专题:函数的性质及应用,导数的综合应用
分析:根据条件得到M、N横坐标相等,将恒成立问题转化为求函数的最值问题.利用函数最值和导数之间的关系即可得到结论.
解答:
解:∵由
=λ
+(1-λ)
,
∴B,N,A三点共线,
又由x=λx1+(1-λ)x2与向量
=λ
+(1-λ)
,得N与M的横坐标相同.
∵在[0,1]上,
∴x1=0,x2=1,
即A(0,0),B(1,1),
则AB方程为y=x,
则|
|=
-x,
设g(x)=
-x,
则g′(x)=
-1=
,
由g′(x)=0,解得x=
,
则x=
是函数g(x)的极大值,同时也是最大值,
则gmax(
)=
-
=
-
=
,
设m(x)=
-x,
则m′(x)=
x-
-1=
-1=
,
由m′(x)=0得,x=
,
此时m(x)取得极大值,同时也是最大值,
则m(
)=
-
=
-
=
,
要使函数y=
与y=
在[0,1]上有且仅有一个“k阶线性近似”,
则
≤k≤
,
故实数k的取值范围为k∈[
,
),
故答案为:k∈[
,
).
| ON |
| OA |
| OB |
∴B,N,A三点共线,
又由x=λx1+(1-λ)x2与向量
| ON |
| OA |
| OB |
∵在[0,1]上,
∴x1=0,x2=1,
即A(0,0),B(1,1),
则AB方程为y=x,
则|
| MN |
| x |
设g(x)=
| x |
则g′(x)=
| 1 | ||
2
|
1-2
| ||
2
|
由g′(x)=0,解得x=
| 1 |
| 4 |
则x=
| 1 |
| 4 |
则gmax(
| 1 |
| 4 |
|
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
设m(x)=
| 3 | x |
则m′(x)=
| 1 |
| 3 |
| 2 |
| 3 |
| 1 | |||
3
|
1-3
| |||
3
|
由m′(x)=0得,x=
| ||
| 9 |
此时m(x)取得极大值,同时也是最大值,
则m(
| ||
| 9 |
| 3 |
| ||||
| ||
| 9 |
| ||
| 3 |
| ||
| 9 |
2
| ||
| 9 |
要使函数y=
| x |
| 3 | x |
则
| 1 |
| 4 |
2
| ||
| 9 |
故实数k的取值范围为k∈[
| 1 |
| 4 |
2
| ||
| 9 |
故答案为:k∈[
| 1 |
| 4 |
2
| ||
| 9 |
点评:点评:本题考查新定义,解答的关键是将已知条件进行转化,同时应注意恒成立问题的处理策略.运算量较大,有一定的难度.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知a>0,b>0,若不等式mab≤(3a+b)(b+3a)恒成立,则m的最大值等于( )
| A、12 | B、9 | C、6 | D、3 |
设z=
+(1-i)2,则(1+x)4(1+zx)3展开式中x5项的系数是( )
| 1+i |
| 1-i |
| A、-2-3i |
| B、-12+3i |
| C、1+21i |
| D、-35i |
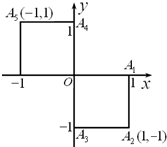 甲、乙、丙三人中要选一人去参加唱歌比赛,于是他们制定了一个规则,规则为:(如图)以O为起点,再从A1,A2,A3,A4,A5,这5个点中任取两点分别为终点得到两个向量,记这两个向量的数量积为X,若X>0就让甲去;若X=0就让乙去;若X<0就是丙去.
甲、乙、丙三人中要选一人去参加唱歌比赛,于是他们制定了一个规则,规则为:(如图)以O为起点,再从A1,A2,A3,A4,A5,这5个点中任取两点分别为终点得到两个向量,记这两个向量的数量积为X,若X>0就让甲去;若X=0就让乙去;若X<0就是丙去.