题目内容
已知椭圆C：
+
=1（a＞b＞0）过点（
，
），椭圆C左右焦点分别为F1，F2，上顶点为E，△EF1F2为等边三角形．定义椭圆C上的点M（x0，y0）的“伴随点”为N（
，
）．
（1）求椭圆C的方程；
（2）求tan∠MON的最大值；
（3）直线l交椭圆C于A、B两点，若点A、B的“伴随点”分别是P、Q，且以PQ为直径的圆经过坐标原点O．椭圆C的右顶点为D，试探究△OAB的面积与△ODE的面积的大小关系，并证明．
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| ||
| 2 |
| x0 |
| a |
| y0 |
| b |
（1）求椭圆C的方程；
（2）求tan∠MON的最大值；
（3）直线l交椭圆C于A、B两点，若点A、B的“伴随点”分别是P、Q，且以PQ为直径的圆经过坐标原点O．椭圆C的右顶点为D，试探究△OAB的面积与△ODE的面积的大小关系，并证明．
考点：直线与圆锥曲线的综合问题
专题：圆锥曲线中的最值与范围问题
分析：（1）由已知
，由此能求出椭圆C的方程．
（2）设kOM=
=k（k＞0），于是kON=
，由此利用均值定理能求出tan∠MON的最大值．
（3）设A（x1，y1），B（x2，y2），则P(
，
)， Q(
，
)．当直线l的斜率存在时，设方程为y=kx+m，由
得：（3+4k2）x2+8kmx+4（m2-3）=0，由此求出S△OAB=
|AB|d=
；当直线l的斜率不存在时，设方程为x=m（-2＜m＜2）联立椭圆方程得：y2=
，由此求出△OAB的面积是定值
，又△ODE的面积也为
，从而得到△OAB的面积与△ODE的面积相等．
|
（2）设kOM=
| y0 |
| x0 |
| 2k | ||
|
（3）设A（x1，y1），B（x2，y2），则P(
| x1 |
| 2 |
| y1 | ||
|
| x2 |
| 2 |
| y2 | ||
|
|
| 1 |
| 2 |
| 3 |
| 3(4-m2) |
| 4 |
| 3 |
| 3 |
解答：
本小题满分（16分）（第1小题满分（4分），第2小题满分（4分），第3小题满分8分）
解：（1）由已知
，
解得a2=4，b2=3，
∴椭圆C的方程为
+
=1…（4分）
（2）当x0y0=0时，显然tan∠MON=0，
由椭圆对称性，只研究x0＞0，y0＞0即可，
设kOM=
=k（k＞0），于是kON=
…（5分）
tan∠MON=
=
≤
，
（当且仅当k2=
时取等号），
∴tan∠MON的最大值为
．…（8分）
（3）设A（x1，y1），B（x2，y2），则P(
，
)， Q(
，
)；
1）当直线l的斜率存在时，设方程为y=kx+m，
由
得：（3+4k2）x2+8kmx+4（m2-3）=0；
有
①…（10分）
由以PQ为直径的圆经过坐标原点O可得：3x1x2+4y1y2=0；
整理得：(3+4k2)x1x2+4mk(x1+x2)+4m2=0②
将①式代入②式得：3+4k2=2m2，…（12分）
∵3+4k2＞0，∴m2＞0，△=48m2＞0，
又点O到直线y=kx+m的距离d=
∴|AB|=
|x1-x2|=
•
=
•
=
•
所以S△OAB=
|AB|d=
…（14分）
2）当直线l的斜率不存在时，设方程为x=m（-2＜m＜2）
联立椭圆方程得：y2=
；
代入3x1x2+4y1y2=0得3m2-
=0；
m=±
，y=±
，S△OAB=
|AB|d=
|m||y1-y2|=
，
综上：△OAB的面积是定值
又△ODE的面积也为
，
∴△OAB的面积与△ODE的面积相等．…（16分）
解：（1）由已知
|
解得a2=4，b2=3，
∴椭圆C的方程为
| x2 |
| 4 |
| y2 |
| 3 |
（2）当x0y0=0时，显然tan∠MON=0，
由椭圆对称性，只研究x0＞0，y0＞0即可，
设kOM=
| y0 |
| x0 |
| 2k | ||
|
tan∠MON=
| ||||
1+
|
2-
| ||||
|
2-
| ||||
2
|
（当且仅当k2=
| ||
| 2 |
∴tan∠MON的最大值为
2-
| ||||
2
|
（3）设A（x1，y1），B（x2，y2），则P(
| x1 |
| 2 |
| y1 | ||
|
| x2 |
| 2 |
| y2 | ||
|
1）当直线l的斜率存在时，设方程为y=kx+m，
由
|
有
|
由以PQ为直径的圆经过坐标原点O可得：3x1x2+4y1y2=0；
整理得：(3+4k2)x1x2+4mk(x1+x2)+4m2=0②
将①式代入②式得：3+4k2=2m2，…（12分）
∵3+4k2＞0，∴m2＞0，△=48m2＞0，
又点O到直线y=kx+m的距离d=
| |m| | ||
|
∴|AB|=
| 1+k2 |
| 1+k2 |
4
| ||||
| 3+4k2 |
=
| 1+k2 |
4
| ||
| 3+4k2 |
| 1+k2 |
4
| ||
| 2m2 |
所以S△OAB=
| 1 |
| 2 |
| 3 |
2）当直线l的斜率不存在时，设方程为x=m（-2＜m＜2）
联立椭圆方程得：y2=
| 3(4-m2) |
| 4 |
代入3x1x2+4y1y2=0得3m2-
| 3(4-m2) |
| 4 |
m=±
2
| ||
| 5 |
2
| ||
| 5 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
综上：△OAB的面积是定值
| 3 |
又△ODE的面积也为
| 3 |
∴△OAB的面积与△ODE的面积相等．…（16分）
点评：本题考查椭圆方程的求法，考查正切的最大值的求法，考查两个三角形面积的判断，解题时要认真审题，注意点到直线的距离公式和弦长公式的合理运用．
练习册系列答案
相关题目
正六棱锥P-ABCDEF中，G为PB的中点，则三棱锥D-GAC与三棱锥E-GAC的体积比
为（ ）
| VD-GAC |
| VE-GAC |
A、
| ||
| B、1 | ||
C、
| ||
| D、2 |
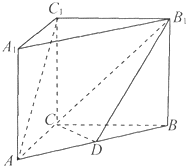如图，在三棱柱ABC-A1B1C1中，C1C⊥底面ABC，AC=BC=CC1=2，AC⊥BC，点D是AB的中点．