题目内容
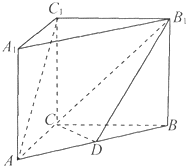 如图,在三棱柱ABC-A1B1C1中,C1C⊥底面ABC,AC=BC=CC1=2,AC⊥BC,点D是AB的中点.
如图,在三棱柱ABC-A1B1C1中,C1C⊥底面ABC,AC=BC=CC1=2,AC⊥BC,点D是AB的中点.(Ⅰ)求证:AC1∥平面CDB1;
(Ⅱ)求四面体B1C1CD的体积.
考点:棱柱、棱锥、棱台的体积,直线与平面平行的判定
专题:综合题,空间位置关系与距离
分析:(Ⅰ)连结BC1,设BC1与B1C的交点为E,连接DE,证得DE∥AC1;由线面平行的判定定理即可证明AC1∥平面CDB1;
(Ⅱ)在平面ABC内作DF⊥BC于点F,可以证明DF是三棱锥D-CC1B1的高,再由锥体体积公式即可求解.
(Ⅱ)在平面ABC内作DF⊥BC于点F,可以证明DF是三棱锥D-CC1B1的高,再由锥体体积公式即可求解.
解答:
(Ⅰ)证明:连结BC1,设BC1与B1C的交点为E,连结DE.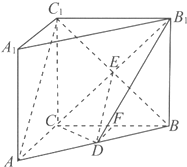
∵三棱柱ABC-A1B1C1,CC1⊥底面ABC,
CC1=BC=2,
∴四边形BCC1B1为正方形.
∴E为BC1中点.
∵D是AB的中点,
∴DE∥AC1.
∵DE?平面CDB1,AC1?平面CDB1,
∴AC1∥平面CDB1. (4分)
(Ⅱ)解:在平面ABC内作DF⊥BC于点F,
∵CC1⊥平面ACB
DF?平面ACB,
∴CC1⊥DF.
∵BC∩CC1=C
∴DF⊥平面BCC1B1.
∴DF是三棱锥D-CC1B1的高,
∵AC=BC=CC1=2
∴S△B1C1C=2,DF=1.
∴四面体B1C1CD的体积为VD-B1C1C=
S△B1C1C•h=
. (9分)

∵三棱柱ABC-A1B1C1,CC1⊥底面ABC,
CC1=BC=2,
∴四边形BCC1B1为正方形.
∴E为BC1中点.
∵D是AB的中点,
∴DE∥AC1.
∵DE?平面CDB1,AC1?平面CDB1,
∴AC1∥平面CDB1. (4分)
(Ⅱ)解:在平面ABC内作DF⊥BC于点F,
∵CC1⊥平面ACB
DF?平面ACB,
∴CC1⊥DF.
∵BC∩CC1=C
∴DF⊥平面BCC1B1.
∴DF是三棱锥D-CC1B1的高,
∵AC=BC=CC1=2
∴S△B1C1C=2,DF=1.
∴四面体B1C1CD的体积为VD-B1C1C=
| 1 |
| 3 |
| 2 |
| 3 |
点评:本题考查线面平行的判定定理、空间几何体的体积,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
用反证法证明命题:设x、y、z∈R+,a=x+
,b=y+
,c=z+
,则a、b、c三个数至少有一个不小于2,下列假设中正确的是( )
| 1 |
| y |
| 1 |
| z |
| 1 |
| x |
| A、假设a,b,c三个数至少有一个不大于2 |
| B、假设a,b,c三个数都不小于2 |
| C、假设a,b,c三个数至多有一个不大于2 |
| D、假设a,b,c三个数都小于2 |
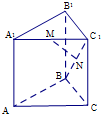 在直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=BC=AA1=2,M,N分别是A1C1,BC1的中点.
在直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=BC=AA1=2,M,N分别是A1C1,BC1的中点.