题目内容

已知f（x）=cos（2x-
π
3
）+sin2x-cos2x
（1）求f（x）的对称轴及对称中心；
（2）若f（α）=
3
5
，2α是第二象限角，求sin2α的值．
考点：三角函数中的恒等变换应用,二倍角的正弦
专题：三角函数的求值,三角函数的图像与性质
分析：（1）将三角函数进行化简，根据三角函数的图象和性质即可求f（x）的对称轴及对称中心；
（2）利用三角函数的倍角公式进行化简即可得到结论．
解答： 解：f(x)=cos(2x-
π
3
)+sin2x-cos2x=
1
2
cos2x+
3
2
sin2x-cos2x=
3
2
sin2x-
1
2
cos2x=sin(2x-
π
6
)
（1）由2x-
π
6
=2kπ+
π
2
，k∈Z，得x=
π
12
+
kπ
2
；
由 2x-
π
6
=kπ得x=
π
12
+
kπ
2
，
故f（x）的对称轴为x=
π
12
+
kπ
2
；对称中心为（
π
12
+
kπ
2
，0）．
（2）若f(α)=
3
5
，即sin(2α-
π
6
)=
3
5
，
则cos(2α-
π
6
)=±
1-sin2(2α-
π
6
)
=±
4
5

又2α在第二象限，即2α∈(2kπ+
π
2
，2k+π)，k∈Z，
则2α-
π
6
∈(2kπ+
π
3
，2k+
5
6
π)，k∈Z，
从而有-
3
2
＜cos(2α-
π
6
)＜
1
2

所以cos(2α-
π
6
)=-
4
5
，
故sin2α=sin[(2α-
π
6
)+
π
6
]=sin(2α-
π
6
)cos
π
6
+cos(2α-
π
6
)sin
π
6
=
3
3
-4
10
点评：本题主要考查三角函数的图象和性质，以及三角函数求值，利用三角公式进行化简是解决本题的关键．要求熟练掌握三角函数的图象和性质．
练习册系列答案
相关题目
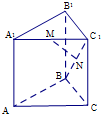在直三棱柱ABC-A1B1C1中，∠ABC=90°，AB=BC=AA1=2，M，N分别是A1C1，BC1的中点．
（1）求证：MN∥平面A1ABB1；
（2）求多面体M-B1C1B的体积．
已知椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）过点（
3
，
3
2
），椭圆C左右焦点分别为F1，F2，上顶点为E，△EF1F2为等边三角形．定义椭圆C上的点M（x0，y0）的“伴随点”为N（
x0
a
，
y0
b
）．
（1）求椭圆C的方程；
（2）求tan∠MON的最大值；
（3）直线l交椭圆C于A、B两点，若点A、B的“伴随点”分别是P、Q，且以PQ为直径的圆经过坐标原点O．椭圆C的右顶点为D，试探究△OAB的面积与△ODE的面积的大小关系，并证明．
已知圆C的极坐标方程为
2
ρ=4sin（θ+
π
4
），以极点为原点，极轴为x轴的正半轴建立平面直角坐标系，直线l的参数方程为
x=3+t
y=1-2t
，（t为参数）
（Ⅰ）将圆C的极坐标方程化为直角坐标方程，直线l的参数方程化为普通方程；
（Ⅱ）判断直线l和圆C的位置关系．
已知函数f（x）=ex（e为自然对数的底），g（x）=ln（f（x）+a）（a为常数），g（x）是实数集R上的奇函数．
（1）求证：f（x）≥x+1（x∈R）；
（2）讨论关于x的方程：lng（x）=g（x）•（x2-2ex+m）（m∈R）的根的个数．
已知椭圆F：
x2
a2
-
y2
b2
=1（a＞b＞0）经过D（2，0），E（1，
3
2
）两点．
（I）求椭圆F的方程；
（Ⅱ）若直线l：y=kx+m与F交于不同两点A，B，点G是线段AB中点，点O为坐标原点，设射线OG交F于点Q，且
OQ
=2
OG
．
①证明：4m2=4k2+1；
②求△AOB的面积．
已知数列{an}的前n项和Sn=n2+4n（n∈N*）．
（1）求数列{an}的通项公式；
（2）若b1=3，且bn+1-bn=an（n∈N*），求数列{
1
bn
}的前n项和Tn．
已知
a
=（2cosx+2
3
sinx，1），
b
=（y，cosx），且
a
∥
b
．
（1）将y表示成x的函数f（x），并求f（x）的最小正周期；
（2）在△ABC中，角A，B，C所对的边分别为a，b，c，若f（B）=3，
BA
•
BC
=
9
2
，且a+c=3+
3
，求边长b．
已知集合A={x|-2≤x≤4}，B={x|x＜a}，且满足A∩B=A，求实数a的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网