题目内容
正六棱锥P-ABCDEF中，G为PB的中点，则三棱锥D-GAC与三棱锥E-GAC的体积比
为（ ）
| VD-GAC |
| VE-GAC |
A、
| ||
| B、1 | ||
C、
| ||
| D、2 |
考点：棱柱、棱锥、棱台的体积
专题：计算题,空间位置关系与距离
分析：由题意，
=
=
=
，利用AC=
CD，即可得出结论．
| VD-GAC |
| VE-GAC |
| VG-DAC |
| VG-EAC |
| S△DAC |
| S△EAC |
| ||||
|
| 3 |
解答：
解：由题意，
=
=
=
∵AC=
CD，
∴
=
，
∴
=
．
故选：C．
| VD-GAC |
| VE-GAC |
| VG-DAC |
| VG-EAC |
| S△DAC |
| S△EAC |
| ||||
|
∵AC=
| 3 |
∴
| ||||
|
| 2 |
| 3 |
∴
| VD-GAC |
| VE-GAC |
| 2 |
| 3 |
故选：C．
点评：利用转换底面的方法求解体积是关键．
练习册系列答案
相关题目
函数f（x）=cos3x+sin2x-cosx，在[0，2π）上的最大值为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
用反证法证明命题：设x、y、z∈R+，a=x+
，b=y+
，c=z+
，则a、b、c三个数至少有一个不小于2，下列假设中正确的是（ ）
| 1 |
| y |
| 1 |
| z |
| 1 |
| x |
| A、假设a，b，c三个数至少有一个不大于2 |
| B、假设a，b，c三个数都不小于2 |
| C、假设a，b，c三个数至多有一个不大于2 |
| D、假设a，b，c三个数都小于2 |
对于函数f（x）=eax-lnx（a是实常数），下列结论正确的一个是（ ）
A、a=1时，f（x）有极大值，且极大值点x0∈（
| ||
B、a=2时，f（x）有极小值，且极小值点x0∈（0，
| ||
C、a=
| ||
| D、a＜0时，f（x）有极大值，且极大值点x0∈（-∞，0） |
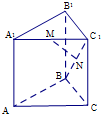在直三棱柱ABC-A1B1C1中，∠ABC=90°，AB=BC=AA1=2，M，N分别是A1C1，BC1的中点．