题目内容
已知函数f(x)=ex-x
(1)求f(x)在点(0,1)处的切线方程;
(2)若F(x)=f(x)-ax2-1的导函数F′(x)在(0,2)上单调,求实数a的取值范围;
(3)对m≥0,n≥0,试比较f(m)+f(n)与mn+2的大小,并说明理由.
(1)求f(x)在点(0,1)处的切线方程;
(2)若F(x)=f(x)-ax2-1的导函数F′(x)在(0,2)上单调,求实数a的取值范围;
(3)对m≥0,n≥0,试比较f(m)+f(n)与mn+2的大小,并说明理由.
考点:利用导数研究函数的单调性,利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:(1)由f′(x)=ex-1,得f′(0)=0,又f(0)=1,故切线方程为:y-1=f′(0)(x-0),即y-1=0.
(2)当F′(x)=ex-2ax-1在[0,2]上是增函数时,有F″(x)=ex-2a≥0在[0,2]上恒成立,即a≤
在[0,2]上恒成立,得a≤
.当F′(x)=ex-2ax-1在[0,2]上是减函数时,得a≥
.综上,a∈[
,+∞)∪(-∞,
].
(3)结论:f(m)+f(n)≥mn+2.当a=
时,由(2)可得F″(x)=ex-2a≥0在[0,+∞)上恒成立,F(x)在[0,+∞)上是增函数,得到:f(x)≥
x2+1.从而f(m)+f(n)≥
+2≥mn+2.
(2)当F′(x)=ex-2ax-1在[0,2]上是增函数时,有F″(x)=ex-2a≥0在[0,2]上恒成立,即a≤
| ex |
| 2 |
| 1 |
| 2 |
| ex |
| 2 |
| e2 |
| 2 |
| 1 |
| 2 |
(3)结论:f(m)+f(n)≥mn+2.当a=
| 1 |
| 2 |
| 1 |
| 2 |
| m2+n2 |
| 2 |
解答:
解:(1)由f′(x)=ex-1,得f′(0)=0,又f(0)=1,
故切线方程为:y-1=f′(0)(x-0),即y-1=0.
(2)当F′(x)=ex-2ax-1在[0,2]上是增函数时,
有F″(x)=ex-2a≥0在[0,2]上恒成立,即a≤
在[0,2]上恒成立,
∴a≤
.
当F′(x)=ex-2ax-1在[0,2]上是减函数时,
有F″(x)=ex-2a≤0在[0,2]上恒成立,即a≥
在[0,2]上恒成立,
∴a≥
.
综上,a∈[
,+∞)∪(-∞,
].
(3)结论:f(m)+f(n)≥mn+2.
当a=
时,由(2)可得F″(x)=ex-2a≥0在[0,+∞)上恒成立,
∴F′(x)在[0,+∞)上是增函数,
∴F′(x)≥F′(0)=0,
∴F(x)在[0,+∞)上是增函数,又F(0)=0,
∴F(x)≥0,得到:f(x)≥
x2+1.
又m≥0,n≥0,故f(m)≥
m2+1,f(n)≥
n2+1,
∴f(m)+f(n)≥
+2≥mn+2,(当且仅当m=n=0时等号成立).
故切线方程为:y-1=f′(0)(x-0),即y-1=0.
(2)当F′(x)=ex-2ax-1在[0,2]上是增函数时,
有F″(x)=ex-2a≥0在[0,2]上恒成立,即a≤
| ex |
| 2 |
∴a≤
| 1 |
| 2 |
当F′(x)=ex-2ax-1在[0,2]上是减函数时,
有F″(x)=ex-2a≤0在[0,2]上恒成立,即a≥
| ex |
| 2 |
∴a≥
| ex |
| 2 |
综上,a∈[
| e2 |
| 2 |
| 1 |
| 2 |
(3)结论:f(m)+f(n)≥mn+2.
当a=
| 1 |
| 2 |
∴F′(x)在[0,+∞)上是增函数,
∴F′(x)≥F′(0)=0,
∴F(x)在[0,+∞)上是增函数,又F(0)=0,
∴F(x)≥0,得到:f(x)≥
| 1 |
| 2 |
又m≥0,n≥0,故f(m)≥
| 1 |
| 2 |
| 1 |
| 2 |
∴f(m)+f(n)≥
| m2+n2 |
| 2 |
点评:本题考察了函数的单调性,切线的方程,参数的范围,考察导数的应用,是一道综合题.

练习册系列答案
相关题目
函数f(x)=cos3x+sin2x-cosx,在[0,2π)上的最大值为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
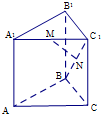 在直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=BC=AA1=2,M,N分别是A1C1,BC1的中点.
在直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=BC=AA1=2,M,N分别是A1C1,BC1的中点.