题目内容
执行如图框图所表达的算法,如果最后输出的s的值为
,那么判断框中实数a的取值范围是( )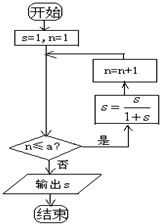
| 1 |
| 10 |

| A、9≤a<10 |
| B、9<a≤10 |
| C、9≤a≤10 |
| D、a>11 |
考点:程序框图
专题:算法和程序框图
分析:执行如图框图所表达的算法,写出每次循环n,s的值,判断退出循环的条件即可确定判断框中实数a的取值范围.
解答:
解:执行如图框图所表达的算法.有
s=1,n=1
n≤a,s=
,n=2
n≤a,s=
,n=3
…
n≤a,s=
,n=9
n≤a,s=
,n=10
此时,n≤a,不成立,退出循环,输出s=
,
故判断框中实数a的取值范围是9≤a<10.
故选:A.
s=1,n=1
n≤a,s=
| 1 |
| 2 |
n≤a,s=
| 1 |
| 3 |
…
n≤a,s=
| 1 |
| 9 |
n≤a,s=
| 1 |
| 10 |
此时,n≤a,不成立,退出循环,输出s=
| 1 |
| 10 |
故判断框中实数a的取值范围是9≤a<10.
故选:A.
点评:本题主要考察了程序框图和算法,属于基础题.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
由①正方形的对角线相等;②矩形的对角线相等;③正方形是矩形,根据“三段论”推理出一个结论,则这个结论是( )
| A、正方形的对角线相等 |
| B、矩形的对角线相等 |
| C、正方形是矩形 |
| D、其它 |
命题“?x>1,使x2-2x-3≤0”的否定形式为( )
| A、?x≤1使x2-2x-3>0 |
| B、?x>1均有x2-2x-3>0 |
| C、?x≤1均有x2-2x-3>0 |
| D、?x≤1使x2-2x-3>0 |
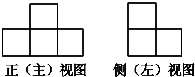 用小正方体搭成一个几何体,如图是它的正(主)视图和侧(左)视图,搭成这个几何体的小正方体最多为
用小正方体搭成一个几何体,如图是它的正(主)视图和侧(左)视图,搭成这个几何体的小正方体最多为