题目内容
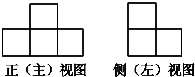用小正方体搭成一个几何体，如图是它的正（主）视图和侧（左）视图，搭成这个几何体的小正方体最多为考点：由三视图求面积、体积
专题：空间位置关系与距离
分析：根据所给出的图形可知这个几何体共有2层，3列，先看第一层正方体可能的最多个数，再看第二层正方体的可能的最多个数，相加即可．
解答：
解：根据主视图和左视图可得：
这个几何体有2层，3列，最底层最多有3×2=6个正方体，第二层有1个正方体，
则搭成这个几何体的小正方体的个数最多是6+1=7个；
故答案为：7
这个几何体有2层，3列，最底层最多有3×2=6个正方体，第二层有1个正方体，
则搭成这个几何体的小正方体的个数最多是6+1=7个；
故答案为：7
点评：此题考查了有三视图判断几何体，关键是根据主视图和左视图确定组合几何体的层数及列数．
练习册系列答案
相关题目
已知函数y=f（x）在区间（a，b）内可导，且x0∈（a，b），则
=（ ）
| lim |
| h→∞ |
| f(x0+h)-f(x0-h) |
| h |
| A、f′（x0） |
| B、2f′（x0） |
| C、-2f′（x0） |
| D、0 |
下列推导错误的是（ ）
| A、α∥β，a?α⇒a∥β |
| B、a∥b，a⊥α⇒b⊥α |
| C、a∥b，b?α⇒a∥α |
| D、a⊥α，a?β⇒α⊥β |
已知直线Ax+By+C=0在x轴的截距大于在y轴的截距，则A、B、C应满足条件（ ）
| A、A＞B | ||||
| B、A＜B | ||||
C、
| ||||
D、
|
在△ABC中，角A、B、C所对的边分别为a、b、c，且BC边上的高为
a，则
+
的最大值是（ ）
| ||
| 6 |
| c |
| b |
| b |
| c |
| A、8 | ||
| B、6 | ||
C、3
| ||
| D、4 |
执行如图框图所表达的算法，如果最后输出的s的值为
，那么判断框中实数a的取值范围是（ ）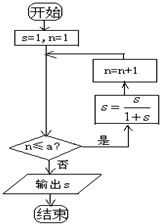
| 1 |
| 10 |
| A、9≤a＜10 |
| B、9＜a≤10 |
| C、9≤a≤10 |
| D、a＞11 |