题目内容
函数y=x2-4x+1,x∈[0,5]的值域为 .
考点:二次函数在闭区间上的最值
专题:函数的性质及应用
分析:首先对二次函数关系式进行变换,然后根据对称轴与开口方向,自变量x距离对称轴距离越远对应的函数值越大,求出结果
解答:
解:函数y=x2-4x+1=(x-2)2-3,x∈[0,5],
由于二次函数的开口方向向上,自变量x距离对称轴距离越远对应的函数值越大.
∴在x=2时ymin=-3,
在x=5时ymax=6,
故答案为:[-3,6].
由于二次函数的开口方向向上,自变量x距离对称轴距离越远对应的函数值越大.
∴在x=2时ymin=-3,
在x=5时ymax=6,
故答案为:[-3,6].
点评:本题考查的知识点:二次函数一般式与顶点式的变换,对称轴与开口方向,自变量x距离对称轴距离越远对应的函数值越大,函数的值域及相关的运算问题.

练习册系列答案
相关题目
已知直线Ax+By+C=0在x轴的截距大于在y轴的截距,则A、B、C应满足条件( )
| A、A>B | ||||
| B、A<B | ||||
C、
| ||||
D、
|
已知集合M={x|x=
,k∈Z},集合N={x|x=
,k∈Z},则( )
| k |
| 4 |
| k |
| 8 |
| A、M∩N=∅ | B、M⊆N |
| C、N⊆M | D、M∪N=N |
执行如图框图所表达的算法,如果最后输出的s的值为
,那么判断框中实数a的取值范围是( )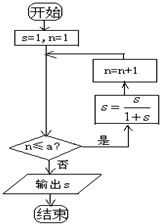
| 1 |
| 10 |

| A、9≤a<10 |
| B、9<a≤10 |
| C、9≤a≤10 |
| D、a>11 |
已知函数f(x)=ax3+3x2+2,若f′(-1)=4,则a的值等于( )
A、
| ||
B、
| ||
C、
| ||
D、
|
在△ABC中,角A,B,C所对的边分别为a,b,c,设
=(1.1),
(-cosA,sinA),记f(A)=
•
.
(1)求f(A)的取值范围
(2)若
与
的夹角为
,C=
,c=
,求b的值.
| m |
| n |
| m |
| n |
(1)求f(A)的取值范围
(2)若
| m |
| n |
| π |
| 3 |
| π |
| 3 |
| 6 |
-315°化为弧度是( )
A、-
| ||
B、-
| ||
C、-
| ||
D、-
|
有一串彩旗,▼代表蓝色,▽代表黄色.两种彩旗排成一行:
▽▼▽▼▼▽▼▼▼▽▼▽▼▼▽▼▼▼▽▼▽▼▼▽▼▼▼…
那么在前200个彩旗中有( )个黄旗.
▽▼▽▼▼▽▼▼▼▽▼▽▼▼▽▼▼▼▽▼▽▼▼▽▼▼▼…
那么在前200个彩旗中有( )个黄旗.
| A、111 | B、89 |
| C、133 | D、67 |