题目内容
命题“?x＞1，使x2-2x-3≤0”的否定形式为（ ）
| A、?x≤1使x2-2x-3＞0 |
| B、?x＞1均有x2-2x-3＞0 |
| C、?x≤1均有x2-2x-3＞0 |
| D、?x≤1使x2-2x-3＞0 |
考点：命题的否定
专题：简易逻辑
分析：特称命题的否定是全称命题写出结果即可．
解答：
解：特称命题的否定是全称命题，
所以命题“?x＞1，使x2-2x-3≤0”的否定形式为：?x＞1均有x2-2x-3＞0．
故选：B．
所以命题“?x＞1，使x2-2x-3≤0”的否定形式为：?x＞1均有x2-2x-3＞0．
故选：B．
点评：本题考查命题的否定，注意特称命题与全称命题的否定关系．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
在△ABC中，角A、B、C所对的边分别为a、b、c，且BC边上的高为
a，则
+
的最大值是（ ）
| ||
| 6 |
| c |
| b |
| b |
| c |
| A、8 | ||
| B、6 | ||
C、3
| ||
| D、4 |
执行如图框图所表达的算法，如果最后输出的s的值为
，那么判断框中实数a的取值范围是（ ）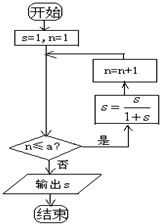
| 1 |
| 10 |
| A、9≤a＜10 |
| B、9＜a≤10 |
| C、9≤a≤10 |
| D、a＞11 |
在△ABC中，角A，B，C所对的边分别为a，b，c，设
=（1.1），
（-cosA，sinA），记f（A）=
•
．
（1）求f（A）的取值范围
（2）若
与
的夹角为
，C=
，c=
，求b的值．
| m |
| n |
| m |
| n |
（1）求f（A）的取值范围
（2）若
| m |
| n |
| π |
| 3 |
| π |
| 3 |
| 6 |
-315°化为弧度是（ ）
A、-
| ||
B、-
| ||
C、-
| ||
D、-
|
有一串彩旗，▼代表蓝色，▽代表黄色．两种彩旗排成一行：
▽▼▽▼▼▽▼▼▼▽▼▽▼▼▽▼▼▼▽▼▽▼▼▽▼▼▼…
那么在前200个彩旗中有（ ）个黄旗．
▽▼▽▼▼▽▼▼▼▽▼▽▼▼▽▼▼▼▽▼▽▼▼▽▼▼▼…
那么在前200个彩旗中有（ ）个黄旗．
| A、111 | B、89 |
| C、133 | D、67 |