题目内容
已知f(x)=x2+2xf'(1),则f(x)在x=-
的切线方程为 .
| 1 |
| 2 |
考点:利用导数研究曲线上某点切线方程,导数的运算
专题:计算题,导数的概念及应用
分析:求导函数,求出f′(1)的值,可得函数的解析式,从而可得切线的斜率与切点的坐标,即可求出切线方程
解答:
解:∵f(x)=x2+2xf′(1),
∴f′(x)=2x+2f′(1),
∴f′(1)=2+2f′(1),
解得f′(1)=-2,
∴f(x)=x2-4x,f′(x)=2x-4,
∴f(-
)=
,f′(-
)=-5,
∴函数在x=-
的切线方程为y-
=-5(x+
),即20x+4y+1=0,
故答案为:20x+4y+1=0.
∴f′(x)=2x+2f′(1),
∴f′(1)=2+2f′(1),
解得f′(1)=-2,
∴f(x)=x2-4x,f′(x)=2x-4,
∴f(-
| 1 |
| 2 |
| 9 |
| 4 |
| 1 |
| 2 |
∴函数在x=-
| 1 |
| 2 |
| 9 |
| 4 |
| 1 |
| 2 |
故答案为:20x+4y+1=0.
点评:本题考查导数的几何意义,考查学生的计算能力,确定函数解析式是关键.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
执行如图框图所表达的算法,如果最后输出的s的值为
,那么判断框中实数a的取值范围是( )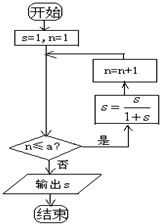
| 1 |
| 10 |

| A、9≤a<10 |
| B、9<a≤10 |
| C、9≤a≤10 |
| D、a>11 |
下列计算正确的是( )
| A、3-1=3 | ||||
B、tan30°=
| ||||
| C、π0=1π | ||||
| D、|-a3|2=a5 |