题目内容
由①正方形的对角线相等；②矩形的对角线相等；③正方形是矩形，根据“三段论”推理出一个结论，则这个结论是（ ）
| A、正方形的对角线相等 |
| B、矩形的对角线相等 |
| C、正方形是矩形 |
| D、其它 |
考点：演绎推理的基本方法
专题：推理和证明
分析：三段论是由两个含有一个共同项的性质判断作前提得出一个新的性质判断为结论的演绎推理．在三段论中，含有大项的前提叫大前提，如本例中的“平行四边形的对角线相等”；含有小项的前提叫小前提，如本例中的“正方形是矩形”叫不前提．另外一个是结论．
解答：
解：由演绎推理三段论可得
“三段论”推理出一个结论，则这个结论是：“正方形的对角线相等”，
故选A．
“三段论”推理出一个结论，则这个结论是：“正方形的对角线相等”，
故选A．
点评：三段论推理是演绎推理中的一种简单判断推理．它包含两个性质判断构成的前提，和一个性质判断构成的结论．一个正确的三段论有仅有三个词项，其中联系大小前提的词项叫中项；出现在大前提中，又在结论中做谓项的词项叫大项；出现在小前提中，又在结论中做主项的词项叫小项．
练习册系列答案
名校课堂系列答案
相关题目
下列推导错误的是（ ）
| A、α∥β，a?α⇒a∥β |
| B、a∥b，a⊥α⇒b⊥α |
| C、a∥b，b?α⇒a∥α |
| D、a⊥α，a?β⇒α⊥β |
已知集合M={x|x=
，k∈Z}，集合N={x|x=
，k∈Z}，则（ ）
| k |
| 4 |
| k |
| 8 |
| A、M∩N=∅ | B、M⊆N |
| C、N⊆M | D、M∪N=N |
执行如图框图所表达的算法，如果最后输出的s的值为
，那么判断框中实数a的取值范围是（ ）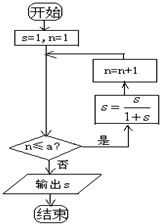
| 1 |
| 10 |
| A、9≤a＜10 |
| B、9＜a≤10 |
| C、9≤a≤10 |
| D、a＞11 |
已知函数f（x）=ax3+3x2+2，若f′（-1）=4，则a的值等于（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
-315°化为弧度是（ ）
A、-
| ||
B、-
| ||
C、-
| ||
D、-
|
设Sn是等差数列{an}的前n项和，若a5=10a3，则
的值为（ ）
| S9 |
| S5 |
A、
| ||
| B、18 | ||
| C、1 | ||
D、
|