题目内容
已知函数f(x)=lnx-
,其中a为常数,且a>0.
(1)若曲线y=f(x)在点(1,f(1))处的切线与直线y=x+1垂直,求函数f(x)的单调递减区间;
(2)若函数f(x)在区间[1,3]上的最小值为
,求a的值.
| x-a |
| x |
(1)若曲线y=f(x)在点(1,f(1))处的切线与直线y=x+1垂直,求函数f(x)的单调递减区间;
(2)若函数f(x)在区间[1,3]上的最小值为
| 1 |
| 3 |
考点:利用导数研究曲线上某点切线方程,利用导数研究函数的单调性,利用导数求闭区间上函数的最值
专题:计算题,分类讨论,导数的综合应用
分析:(1)求出导数,由直线垂直的条件得f'(1)=-1,即可得到a,再令导数小于0,解出即可,注意定义域;
(2)对a讨论,①当0<a≤1时,②当1<a<3时,③当a≥3时,运用导数判断单调性,求出最小值,解方程,即可得到a的值.
(2)对a讨论,①当0<a≤1时,②当1<a<3时,③当a≥3时,运用导数判断单调性,求出最小值,解方程,即可得到a的值.
解答:
解:f′(x)=
-
=
(x>0),
(1)因为曲线y=f(x)在点(1,f(1))处的切线与直线y=x+1垂直,
所以f'(1)=-1,即1-a=-1解得a=2;
当a=2时,f(x)=lnx-
,f′(x)=
.
令f′(x)=
<0,解得0<x<2,
所以函数的递减区间为(0,2);
(2)①当0<a≤1时,f'(x)>0在(1,3)上恒成立,
这时f(x)在[1,3]上为增函数
则f(x)min=f(1)=a-1
令 a-1=
,得a=
>1(舍去),
②当1<a<3时,由f'(x)=0得,x=a∈(1,3)
由于对于x∈(1,a)有f'(x)<0,f(x)在[1,a]上为减函数,
对于x∈(a,3)有f'(x)>0,f(x)在[a,3]上为增函数,
则f(x)min=f(a)=lna,
令lna=
,得a=e
,
③当a≥3时,f'(x)<0在(1,3)上恒成立,这时f(x)在[1,3]上为减函数,
故f′(x)min=f(3)=ln3+
-1.
令ln3+
-1=
得 a=4-3ln3<2(舍去)
综上,a=e
.
| 1 |
| x |
| x-(x-a) |
| x2 |
| x-a |
| x2 |
(1)因为曲线y=f(x)在点(1,f(1))处的切线与直线y=x+1垂直,
所以f'(1)=-1,即1-a=-1解得a=2;
当a=2时,f(x)=lnx-
| x-2 |
| x |
| x-2 |
| x2 |
令f′(x)=
| x-2 |
| x2 |
所以函数的递减区间为(0,2);
(2)①当0<a≤1时,f'(x)>0在(1,3)上恒成立,
这时f(x)在[1,3]上为增函数
则f(x)min=f(1)=a-1
令 a-1=
| 1 |
| 3 |
| 4 |
| 3 |
②当1<a<3时,由f'(x)=0得,x=a∈(1,3)
由于对于x∈(1,a)有f'(x)<0,f(x)在[1,a]上为减函数,
对于x∈(a,3)有f'(x)>0,f(x)在[a,3]上为增函数,
则f(x)min=f(a)=lna,
令lna=
| 1 |
| 3 |
| 1 |
| 3 |
③当a≥3时,f'(x)<0在(1,3)上恒成立,这时f(x)在[1,3]上为减函数,
故f′(x)min=f(3)=ln3+
| a |
| 3 |
令ln3+
| a |
| 3 |
| 1 |
| 3 |
综上,a=e
| 1 |
| 3 |
点评:本题考查导数的运用:求切线方程和求单调区间、求极值和最值,考查两直线垂直的条件,考查分类讨论的思想方法,属于中档题.

练习册系列答案
相关题目
已知函数y=f(x)在区间(a,b)内可导,且x0∈(a,b),则
=( )
| lim |
| h→∞ |
| f(x0+h)-f(x0-h) |
| h |
| A、f′(x0) |
| B、2f′(x0) |
| C、-2f′(x0) |
| D、0 |
已知直线Ax+By+C=0在x轴的截距大于在y轴的截距,则A、B、C应满足条件( )
| A、A>B | ||||
| B、A<B | ||||
C、
| ||||
D、
|
在△ABC中,角A、B、C所对的边分别为a、b、c,且BC边上的高为
a,则
+
的最大值是( )
| ||
| 6 |
| c |
| b |
| b |
| c |
| A、8 | ||
| B、6 | ||
C、3
| ||
| D、4 |
已知集合M={x|x=
,k∈Z},集合N={x|x=
,k∈Z},则( )
| k |
| 4 |
| k |
| 8 |
| A、M∩N=∅ | B、M⊆N |
| C、N⊆M | D、M∪N=N |
执行如图框图所表达的算法,如果最后输出的s的值为
,那么判断框中实数a的取值范围是( )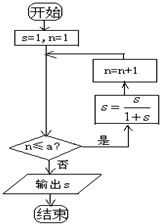
| 1 |
| 10 |

| A、9≤a<10 |
| B、9<a≤10 |
| C、9≤a≤10 |
| D、a>11 |
有一串彩旗,▼代表蓝色,▽代表黄色.两种彩旗排成一行:
▽▼▽▼▼▽▼▼▼▽▼▽▼▼▽▼▼▼▽▼▽▼▼▽▼▼▼…
那么在前200个彩旗中有( )个黄旗.
▽▼▽▼▼▽▼▼▼▽▼▽▼▼▽▼▼▼▽▼▽▼▼▽▼▼▼…
那么在前200个彩旗中有( )个黄旗.
| A、111 | B、89 |
| C、133 | D、67 |