题目内容
若方程lnx+2x-10=0的解为x0,则大于x0的最小整数是 .
考点:函数的零点与方程根的关系
专题:函数的性质及应用
分析:由条件:lnx+2x-10=0得lnx=10-2x,欲求出方程的近似解,利用图解法,分别作出函数y=lnx和y=10-2x的图象,观察交点在(4,5)内,从而得出结论.
解答:
 解:由条件:lnx+2x-10=0得lnx=10-2x,
解:由条件:lnx+2x-10=0得lnx=10-2x,
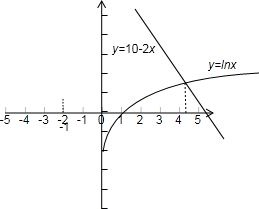
分别作出函数y=lnx和y=10-2x的图象:
观察交点在(4,5)内.
则大于x0的最小整数是5.
故答案为:5.
 解:由条件:lnx+2x-10=0得lnx=10-2x,
解:由条件:lnx+2x-10=0得lnx=10-2x,分别作出函数y=lnx和y=10-2x的图象:
观察交点在(4,5)内.
则大于x0的最小整数是5.
故答案为:5.
点评:本题考查了函数的零点的定义,函数的零点与方程的根的关系,考查了数形结合思想,属于基础题.

练习册系列答案
相关题目
已知全集U=R,A={x|x≤-2},B={x|x≥1},则集合∁U(A∪B)=( )
| A、{x|-2<x<1} |
| B、{x|x≤1} |
| C、{x|-2≤x≤1} |
| D、{x|x≥-2} |
如果A(2,2),B(a,0),C(0,4)三点共线,则a的值是( )
| A、-3 | B、3 | C、4 | D、-4 |