题目内容
 如图,四棱锥P-ABCD的底面是边长为1的正方形,PA⊥CD,PA=1,PD=
如图,四棱锥P-ABCD的底面是边长为1的正方形,PA⊥CD,PA=1,PD=| 2 |
(1)求证:CD∥平面PAB,
(2)求证:PA⊥平面ABCD;
(3)求四棱锥P-ABCD的体积;
(4)求直线PC与平面ABCD所成角的正弦值.
考点:棱柱、棱锥、棱台的体积,直线与平面平行的判定,直线与平面垂直的判定
专题:空间位置关系与距离,空间角
分析:(1)由已知得CD∥AB,由此能证明CD∥平面PAB.
(2)由已知得PA⊥AD,PA⊥CD,AD∩CD=D,由此能证明PA⊥平面ABCD.
(3)由已知得四棱锥P-ABCD的底面积为1,四棱锥P-ABCD的高为1,由此能求出四棱锥P-ABCD的体积.(4)由PA⊥平面ABCD,得∠PCA是直线PC与平面ABCD所成角,由此能求出直线PC与平面ABCD所成角的正弦值.
(2)由已知得PA⊥AD,PA⊥CD,AD∩CD=D,由此能证明PA⊥平面ABCD.
(3)由已知得四棱锥P-ABCD的底面积为1,四棱锥P-ABCD的高为1,由此能求出四棱锥P-ABCD的体积.(4)由PA⊥平面ABCD,得∠PCA是直线PC与平面ABCD所成角,由此能求出直线PC与平面ABCD所成角的正弦值.
解答:
(1)证明:∵四棱锥P-ABCD的底面是边长为1的正方形,
∴CD∥AB,
∵CD不包含于平面PAB,AB?平面PAB,
∴CD∥平面PAB.
(2)证明:∵四棱锥P-ABCD的底面是边长为1的正方形,PA=1,PD=
,
∴PD2=PA2+AD2,
∴PA⊥AD,
又PA⊥CD,AD∩CD=D,
∴PA⊥平面ABCD.
(3)解:∵四棱锥P-ABCD的底面是边长为1的正方形,
∴四棱锥P-ABCD的底面积为1,
∵PA⊥平面ABCD,∴四棱锥P-ABCD的高为1,
∴四棱锥P-ABCD的体积为V=
×1×1=
.
(4)解: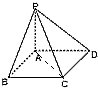 ∵PA⊥平面ABCD,
∵PA⊥平面ABCD,
∴∠PCA是直线PC与平面ABCD所成角,
∵四棱锥P-ABCD的底面是边长为1的正方形,PA=1,
∴AC=
,∴PC=
,
∴sin∠PCA=
=
=
.
∴直线PC与平面ABCD所成角的正弦值为
.
∴CD∥AB,
∵CD不包含于平面PAB,AB?平面PAB,
∴CD∥平面PAB.
(2)证明:∵四棱锥P-ABCD的底面是边长为1的正方形,PA=1,PD=
| 2 |
∴PD2=PA2+AD2,
∴PA⊥AD,
又PA⊥CD,AD∩CD=D,
∴PA⊥平面ABCD.
(3)解:∵四棱锥P-ABCD的底面是边长为1的正方形,
∴四棱锥P-ABCD的底面积为1,
∵PA⊥平面ABCD,∴四棱锥P-ABCD的高为1,
∴四棱锥P-ABCD的体积为V=
| 1 |
| 3 |
| 1 |
| 3 |
(4)解:
 ∵PA⊥平面ABCD,
∵PA⊥平面ABCD,∴∠PCA是直线PC与平面ABCD所成角,
∵四棱锥P-ABCD的底面是边长为1的正方形,PA=1,
∴AC=
| 2 |
| 3 |
∴sin∠PCA=
| PA |
| PC |
| 1 | ||
|
| ||
| 3 |
∴直线PC与平面ABCD所成角的正弦值为
| ||
| 3 |
点评:本题考查CD∥平面PAB的证明,考查PA⊥平面ABCD的证明,考查求四棱锥P-ABCD的体积的求法,考查直线PC与平面ABCD所成角的正弦值的求法,解题时要注意空间思维能力的培养.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
命题“?x0∈R,x02+x0+2<0”的否定是( )
| A、?x0∈R,x02+x0+2≥0 |
| B、?x∈R,x2+x+2≥0 |
| C、?x∈R,x2+x+2<0 |
| D、?x∈R,x2+x+2>0 |
已知tanθ=2,则
=( )
sin(
| ||
sin(
|
| A、2 | ||
| B、-2 | ||
| C、0 | ||
D、
|