题目内容
证明:1+
+
+
+…+
<
.
| 1 |
| 3 |
| 1 |
| 7 |
| 1 |
| 15 |
| 1 |
| 2n-1 |
| 5 |
| 3 |
考点:不等式的证明
专题:不等式
分析:直接利用方所关系式,进一步分情况讨论证明结论成立.
解答:
证明:利用放缩关系式
<
-
,
等价于:2k+1-2<2k+1-1
所以:①当n=1时,原不等式成立,
②当n≥2时,1+
+
+…+
≤1+
(
-
)=1+
-
<
,
由此得到该不等式成立.
| 1 |
| 2k-1 |
| 2 |
| 2k-1 |
| 2 |
| 2k+1-1 |
等价于:2k+1-2<2k+1-1
所以:①当n=1时,原不等式成立,
②当n≥2时,1+
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2k-1 |
| n |
 |
| k=2 |
| 2 |
| 2k-1 |
| 2 |
| 2k+1-1 |
| 2 |
| 3 |
| 2 |
| 2k+1-1 |
| 5 |
| 3 |
由此得到该不等式成立.
点评:本题考查的知识要点:放缩法在不等式中的应用,属于中等题型.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知集合A={1,2},则下列说法正确的是( )
| A、1⊆A | B、{1}∈A |
| C、A⊆{1} | D、Φ⊆A |
已知函数f(x)在定义在R上的奇函数,若对于任意给定的不等实数x1、x2,不等式x1f(x1)+x2f(x2)<x1f(x2)+x2f(x1)恒成立,则不等式f(x)<0的解集为( )
| A、(-∞,0) |
| B、(0,+∞) |
| C、(-∞,10) |
| D、(1,+∞) |
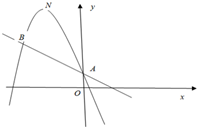 二次函数y=-
二次函数y=- 如图,四棱锥P-ABCD的底面是边长为1的正方形,PA⊥CD,PA=1,PD=
如图,四棱锥P-ABCD的底面是边长为1的正方形,PA⊥CD,PA=1,PD=