题目内容
5.已知正方形ABCD的面积为2,点P在边AB上,则$\overrightarrow{PD}•\overrightarrow{PC}$的最小值为( )| A. | $\frac{{\sqrt{6}}}{2}$ | B. | $\frac{3}{2}$ | C. | 2 | D. | $\sqrt{2}$ |
分析 可画出图形,根据正方形的面积为2可求出边长,结合图形,可得出$\overrightarrow{PD}•\overrightarrow{PC}=(\overrightarrow{AD}-\overrightarrow{AP})•(\overrightarrow{BC}-\overrightarrow{BP})$,进行数量积的运算得出$\overrightarrow{PD}•\overrightarrow{PC}=2-\overrightarrow{AP}•\overrightarrow{PB}$,可设$|\overrightarrow{AP}|=x,|\overrightarrow{PB}|=\sqrt{2}-x$,从而得出$\overrightarrow{PD}•\overrightarrow{PC}={x}^{2}-\sqrt{2}x+2$,配方便可求出最小值.
解答 解:如图,$\overrightarrow{PD}=\overrightarrow{AD}-\overrightarrow{AP}$,$\overrightarrow{PC}=\overrightarrow{BC}-\overrightarrow{BP}$;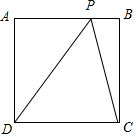 正方形的面积为2,则边长为$\sqrt{2}$;
正方形的面积为2,则边长为$\sqrt{2}$;
∴$\overrightarrow{PD}•\overrightarrow{PC}=(\overrightarrow{AD}-\overrightarrow{AP})•(\overrightarrow{BC}-\overrightarrow{BP})$
=$\overrightarrow{AD}•\overrightarrow{BC}-\overrightarrow{AP}•\overrightarrow{BC}-\overrightarrow{AD}•\overrightarrow{BP}+\overrightarrow{AP}•\overrightarrow{BP}$
=$2-0-0-\overrightarrow{AP}•\overrightarrow{PB}$
=$2-\overrightarrow{AP}•\overrightarrow{PB}$;
设$|\overrightarrow{AP}|=x,0≤x≤\sqrt{2}$,则$|\overrightarrow{PB}|=\sqrt{2}-x$;
∴$\overrightarrow{PD}•\overrightarrow{PC}=2-x(\sqrt{2}-x)$
=${x}^{2}-\sqrt{2}x+2$
=$(x-\frac{\sqrt{2}}{2})^{2}+\frac{3}{2}$;
∴$\overrightarrow{PD}•\overrightarrow{PC}$的最小值为$\frac{3}{2}$.
故选B.
点评 考查向量减法的几何意义,向量数量积的运算及计算公式,配方法求最值.

 阅读快车系列答案
阅读快车系列答案| A. | 定义域是$\{x|x≠kπ+\frac{π}{6},(k∈Z)\}$ | B. | 值域是R | ||
| C. | 在其定义域上是增函数 | D. | 最小正周期是π |
| A. | 0.1 | B. | 0.2 | C. | 0.4 | D. | 0.6 |
| A. | $-\frac{{\sqrt{3}}}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $-\frac{1}{2}$ | D. | $\frac{1}{2}$ |
| A. | -$\overrightarrow{a}$+3$\overrightarrow{b}$ | B. | $\overrightarrow{a}$-3$\overrightarrow{b}$ | C. | 3$\overrightarrow{a}$-$\overrightarrow{b}$ | D. | -3$\overrightarrow{a}$+$\overrightarrow{b}$ |
| A. | $\overrightarrow 0$ | B. | $\overrightarrow{AC}$ | C. | $\overrightarrow{BD}$ | D. | $\overrightarrow{DA}$ |