题目内容
10．二进制数1101100（2）化为十进制数是108．分析 利用1101100（2）=1×26+1×25+1×23+1×22=108（10）．即可得出．
解答 解：1101100（2）=1×26+1×25+1×23+1×22=108（10）．
故答案是：108
点评 本题考查了把“二进制”数化为“十进制”的方法，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
18．已知双曲线的一条渐近线过点$（{2，\sqrt{3}}）$，且双曲线的一个焦点在抛物线${x^2}=4\sqrt{7}y$的准线上，则双曲线的标准方程为（ ）
| A． | $\frac{y^2}{3}-\frac{x^2}{4}=1$ | B． | $\frac{y^2}{4}-\frac{x^2}{3}=1$ | C． | $\frac{x^2}{3}-\frac{y^2}{4}=1$ | D． | $\frac{x^2}{4}-\frac{y^2}{3}=1$ |
5．已知正方形ABCD的面积为2，点P在边AB上，则$\overrightarrow{PD}•\overrightarrow{PC}$的最小值为（ ）
| A． | $\frac{{\sqrt{6}}}{2}$ | B． | $\frac{3}{2}$ | C． | 2 | D． | $\sqrt{2}$ |
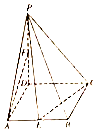如图，在四棱锥P-ABCD中，底面ABCD为菱形，∠DAB=60°，PD⊥平面ABCD，PD=AD=4，点E、F分别为AB和PD的中点．
2．已知集合A={x|x2-x-2≤0}，B=Z，则A∩B=（ ）
| A． | {-1，0，1，2} | B． | {-2，-1，0，1} | C． | {0，1} | D． | {-1，0} |