题目内容
11.已知向量$\overrightarrow{a}$=(0,-1,1),$\overrightarrow{b}$(4,1,0),|λ$\overrightarrow{a}$+$\overrightarrow{b}$|=$\sqrt{29}$且λ>0,则λ=( )| A. | -2 | B. | 2 | C. | -3 | D. | 3 |
分析 对|λ$\overrightarrow{a}$+$\overrightarrow{b}$|=$\sqrt{29}$两边平方,列出方程解出.
解答 解:|$\overrightarrow{a}$|=$\sqrt{2}$,|$\overrightarrow{b}$|=$\sqrt{17}$,$\overrightarrow{a}•\overrightarrow{b}$=-1.
∵|λ$\overrightarrow{a}$+$\overrightarrow{b}$|=$\sqrt{29}$,∴($λ\overrightarrow{a}+\overrightarrow{b}$)2=29.即λ2|$\overrightarrow{a}$|2+2λ$\overrightarrow{a}•\overrightarrow{b}$+|$\overrightarrow{b}$|2=29,∴2λ2-2λ-12=0,∵λ>0,∴λ=3.
故选:D.
点评 本题考查了空间向量的数量积运算,是基础题.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案
相关题目
2.双曲线$\frac{x^2}{a^2}-{y^2}=1$的离心率为$\sqrt{2}$,则正数a的值为( )
| A. | $\sqrt{3}$ | B. | 2 | C. | $\sqrt{2}$ | D. | 1 |
6.已知双曲线$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{9}$=1,是否存在直线l,使其截双曲线所得弦的中点为P(1,1)?若存在,求出直线l的方程;若不存在,说明理由.
16.如图,在△OAB中,点P在边AB上,且AP:PB=3:2.则$\overrightarrow{OP}$=( )


| A. | $\frac{3}{5}\overrightarrow{OA}+\frac{2}{5}\overrightarrow{OB}$ | B. | $\frac{2}{5}\overrightarrow{OA}+\frac{3}{5}\overrightarrow{OB}$ | C. | $\frac{3}{5}\overrightarrow{OA}-\frac{2}{5}\overrightarrow{OB}$ | D. | $\frac{2}{5}\overrightarrow{OA}-\frac{3}{5}\overrightarrow{OB}$ |
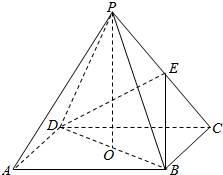 如图,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,E是PC的中点.
如图,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,E是PC的中点.