题目内容

19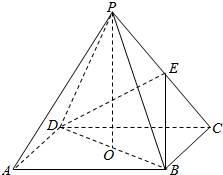．如图，ABCD是正方形，O是正方形的中心，PO⊥底面ABCD，E是PC的中点．
（1）求证：PA∥平面BDE；
（2）若PA=AB=2，求三棱锥D-BEC的体积．

分析 （1）利用中位线的方法在平面内找到与已知直线平行的直线，结合直线与平面平行的判定定理即可得到答案．
（2）利用等体积转化，即可求三棱锥D-BEC的体积．

解答 （1）证明：∵O是AC的中点，E是PC的中点，∴OE∥AP，
又∵OE?平面BDE，PA?平面BDE，∴PA∥平面BDE；
（2）解：由题意，PO=$\sqrt{4-2}$=$\sqrt{2}$，∴E到平面DBC的距离为$\frac{\sqrt{2}}{2}$，
∴三棱锥D-BEC的体积V=$\frac{1}{3}×\frac{1}{2}×2×2×\frac{\sqrt{2}}{2}$=$\frac{\sqrt{2}}{3}$．

点评 本题考查直线与平面平行的判定定理，考查三棱锥D-BEC的体积，考查学生分析解决问题的能力，属于中档题．

练习册系列答案
相关题目
9．已知△ABC的内角A，B，C的对边分别为a，b，c，向量$\vec m=（sinA，a），\vec n=（1，sinB）$
（1）当$\vec m•\vec n=2sinA$时，求b的值；
（2）当$\vec m∥\vec n$时，且$cosC=\frac{1}{2}a$，求tanA•tanB的值．
10．若点P、Q均在椭圆$Γ：\frac{x^2}{a^2}+\frac{y^2}{{{a^2}-1}}=1$（a＞1）上运动，F1、F2是椭圆Γ的左、右焦点，则$|{\overrightarrow{P{F_1}}+\overrightarrow{P{F_2}}-2\overrightarrow{PQ}}|$的最大值为2a．
7．函数$f（x）=\frac{1}{3}{x^3}-{x^2}-3x+5$的零点的个数是（　　）
A．0B．1C．2D．3
14．已知递增的等比数列{an}满足a2+a3+a4=28，且a3+2是a2，a4的等差中项．
（1）求数列{an}的通项公式；
（2）若bn=log2a2n，Sn是数列{bn}的前n项和，求使Sn＞40+4n成立的正整数n的最小值．
4．若抛物线y2=2px（p＞0）的焦点为F，其准线经过双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（a＞0，b＞0）$的左焦点，点M为这两条曲线的一个交点，且|MF|=p，则双曲线的离心率为（　　）
A．$\frac{{2+\sqrt{2}}}{2}$B．$2+\sqrt{2}$C．$1+\sqrt{2}$D．$\frac{{1+\sqrt{2}}}{2}$
11．已知向量$\overrightarrow{a}$=（0，-1，1），$\overrightarrow{b}$（4，1，0），|λ$\overrightarrow{a}$+$\overrightarrow{b}$|=$\sqrt{29}$且λ＞0，则λ=（　　）
A．-2B．2C．-3D．3
8．设 a=sin46°，b=cos46°，c=tan46°．则（　　）
A．c＞a＞bB．a＞b＞cC．b＞c＞aD．c＞b＞a
9．已知椭圆C1：$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$（a＞b＞0）的离心率e=$\frac{\sqrt{5}}{3}$，且椭圆C1的短轴长为4．
（1）求椭圆C1的方程；
（2）若椭圆C1的左右焦点分别为F1、F2，抛物线C2：y2=2px（p＞0）与椭圆C1交于不同两点P、Q．且$\overrightarrow{P{F}_{2}}$=$\overrightarrow{{F}_{2}Q}$．求抛物线C2的准线方程；
（3）若直线l与椭圆C1交于不同两点M、N．且$\overrightarrow{OM}•\overrightarrow{ON}$=0，求证：直线l恒与一个定圆相切，并求出定圆的方程．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网