题目内容
3.已知函数f(x)=$\left\{\begin{array}{l}{|x+1|,x≤0}\\{|lo{g}_{2}x|,x>0}\end{array}\right.$,若方程f(x)=a(a∈R)有四个不同的解x1,x2,x3,x4,且x1<x2<x3<x4,则(x1+x2)x4的取值范围是[-4,-2).分析 由题意作函数f(x)=$\left\{\begin{array}{l}{|x+1|,x≤0}\\{|lo{g}_{2}x|,x>0}\end{array}\right.$与y=a的图象,从而可得x1+x2=-2,0<log2x4≤1,从而解得.
解答 解:由题意作函数f(x)=$\left\{\begin{array}{l}{|x+1|,x≤0}\\{|lo{g}_{2}x|,x>0}\end{array}\right.$与y=a的图象如下, ,
,
结合图象可知,
x1+x2=-2,0<log2x4≤1,
故x1+x2=-2,1<x4≤2,
故-4≤(x1+x2)x4<-2,
故答案为:[-4,-2).
点评 本题考查了数形结合的思想应用及分段函数的应用.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
18.从某学习小组的5名男生和4名女生中任意选取3名学生进行视力检测,其中至少要选到男生与女生各一名,则不同的选取种数有( )
| A. | 35 | B. | 70 | C. | 80 | D. | 140 |
8.设 a=sin46°,b=cos46°,c=tan46°.则( )
| A. | c>a>b | B. | a>b>c | C. | b>c>a | D. | c>b>a |
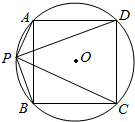 已知:如图,⊙O是正方形ABCD的外接圆,P是$\widehat{AB}$上的一点,求证:$\frac{PA+PC}{PB+PD}$=$\frac{PD}{PC}$.
已知:如图,⊙O是正方形ABCD的外接圆,P是$\widehat{AB}$上的一点,求证:$\frac{PA+PC}{PB+PD}$=$\frac{PD}{PC}$.