题目内容
20.数列{an}的前n项和Sn=100n-n2(n∈N*).(1)判断{an}是不是等差数列,若是,求其首项、公差;
(2)设bn=|an|,求数列{bn}的前n项和.
分析 (1)利用an=Sn-Sn-1求出通项公式,根据通项公式判断.
(2)根据an的通项公式判断an的符号变化,然后对n的范围进行讨论求和.
解答 解:(1)当n=1时,a1=S1=99,当n≥2时,an=Sn-Sn-1=100n-n2-[100(n-1)-(n-1)2]=101-2n,显然当n=1时,an=101-2n也成立.
∴an=101-2n,∴an+1-an=101-2(n+1)-(101-2n)=-2.
∴{an}是等差数列,a1=99,d=-2.
(2)令an≥0,得101-2n≥0,解得n≤50.∴当n≤50时,bn=an,当n≥51时,bn=-an.
设数列{bn}的前n项和为Tn,
∴当n≤50时,Tn=Sn=100n-n2,
当n≥51时,Tn=S50-a51-a52-…-an=S50-(Sn-S50)=2S50-Sn=2(100×50-502)-(100n-n2)=n2-100n+5000.
点评 本题考查了等差数列的判断,数列求和,判断出an的符号变化是关键.

练习册系列答案
相关题目
8.设 a=sin46°,b=cos46°,c=tan46°.则( )
| A. | c>a>b | B. | a>b>c | C. | b>c>a | D. | c>b>a |
10.设P是双曲线$\frac{{x}^{2}}{4}$-y2=1上的意一点,点P到双曲线的两条渐近线的距离分别为d1,d2,则( )
| A. | d1+d2=$\frac{4\sqrt{5}}{5}$ | B. | d1•d2=$\frac{4\sqrt{5}}{5}$ | C. | d1+d2=$\frac{4}{5}$ | D. | d1•d2=$\frac{4}{5}$ |
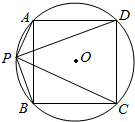 已知:如图,⊙O是正方形ABCD的外接圆,P是$\widehat{AB}$上的一点,求证:$\frac{PA+PC}{PB+PD}$=$\frac{PD}{PC}$.
已知:如图,⊙O是正方形ABCD的外接圆,P是$\widehat{AB}$上的一点,求证:$\frac{PA+PC}{PB+PD}$=$\frac{PD}{PC}$.