题目内容
9．已知等差数列{an}的前n项和为Sn，且a1=1，S3+S4=S5．（Ⅰ）求数列{an}的通项公式；
（Ⅱ）令${b_n}={（-1）^{n-1}}{a_n}$，求数列{bn}的前2n项和T2n．
分析 （Ⅰ）由S3+S4=S5可得：a1+a2+a3=a5，3（1+d）=1+4d，解得d=2，由等差数列的通项公式即可求得{an}的通项公式；
（Ⅱ）${b_n}={（-1）^{n-1}}•（2n-1）$．T2n=1-3+5-7+…+•（2n-3）-（2n-1）=-2n．
解答 解：（Ⅰ）设等差数列{an}的公差为d，
由S3+S4=S5可得：a1+a2+a3=a5，
即3a2=a5，-------（2分）
∴3（1+d）=1+4d，解得d=2．-------（4分）
∴an=1+（n-1）×2=2n-1，
数列{an}的通项公式an=2n-1；-------（6分）
（Ⅱ）由（Ⅰ）可得：${b_n}={（-1）^{n-1}}•（2n-1）$．
∴T2n=1-3+5-7+…+•（4n-3）-（4n-1），
=（-2）×n，
=-2n，
数列{bn}的前2n项和T2n=-2n．------（12分）
点评 本题考查等差数列的通项公式及性质，考查计算能力，属于基础题．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
1．设y=f（t）是某港口水的深度y（米）关于时间t（时）的函数，其中0≤t≤24．下表是该港口某一天从0时至24时记录的时间t与水深y的关系表：
经长期观察，函数y=f（t）的图象可以近似地看成函数y=k+Asin（ωt+φ）的图象．下面的函数中，最能近似表示表中数据间对应关系的函数是（ ）
| t | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| y | 5 | 7.5 | 5 | 2.5 | 5 | 7.5 | 5 | 2.5 | 5 |
| A． | $y=5+\frac{5}{2}sin\frac{π}{12}t，t∈[0，24]$ | B． | $y=5+\frac{5}{2}sin（\frac{π}{12}t+\frac{π}{2}），t∈[0，24]$ | ||
| C． | $y=5+\frac{5}{2}sin\frac{π}{6}t，t∈[0，24]$ | D． | $y=5+\frac{5}{2}sin（\frac{π}{6}t+π），t∈[0，24]$ |
17．已知全集U=R，集合A={x|x＞2}，B={1，2，3，4}，那么（∁UA）∩B=（ ）
| A． | {3，4} | B． | {1，2，3} | C． | {1，2} | D． | {1，2，3，4} |
13．
如图所示，在正方体ABCD-A1B1C1D1中，已知M，N分别是BD和AD的中点，则B1M与D1N所成角的余弦值为（ ）
如图所示，在正方体ABCD-A1B1C1D1中，已知M，N分别是BD和AD的中点，则B1M与D1N所成角的余弦值为（ ）| A． | $\frac{{\sqrt{30}}}{10}$ | B． | $\frac{{\sqrt{30}}}{15}$ | C． | $\frac{{\sqrt{30}}}{30}$ | D． | $\frac{{\sqrt{15}}}{15}$ |
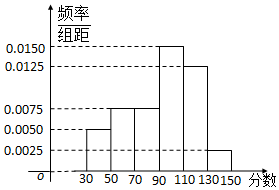从某校高三上学期期末数学考试成绩中，随机抽取了60名学生的成绩得到如图所示的频率分布直方图：