题目内容
已知函数f(x)的定义域为R,且满足f(-x)=
>0,g(x)=f(x)+c(c为常数)在区间[a,b]上是减函数.判断g(x)在[-b,-a]上的单调性.
| 1 |
| f(x) |
考点:利用导数研究函数的单调性
专题:计算题,函数的性质及应用
分析:利用单调性的定义,任取x1、x2∈[-b,-a],且x1<x2,化为已知区间使a≤-x2<-x1≤b,从而由题意化简可得函数的单调性.
解答:
解:任取x1、x2∈[-b,-a],且x1<x2,
则a≤-x2<-x1≤b,
又∵g(x)=f(x)+c(c为常数)在区间[a,b]上是减函数,
∴g(-x2)>g(-x1),
又∵g(x)=f(x)+c,
∴f(-x2)>f(-x1),
又∵f(-x)=
>0,
∴
>
>0,
∴f(x2)<f(x1),
∴g(x2)<g(x1),
∴g(x)在[-b,-a]上也是减函数.
则a≤-x2<-x1≤b,
又∵g(x)=f(x)+c(c为常数)在区间[a,b]上是减函数,
∴g(-x2)>g(-x1),
又∵g(x)=f(x)+c,
∴f(-x2)>f(-x1),
又∵f(-x)=
| 1 |
| f(x) |
∴
| 1 |
| f(x2) |
| 1 |
| f(x1) |
∴f(x2)<f(x1),
∴g(x2)<g(x1),
∴g(x)在[-b,-a]上也是减函数.
点评:本题考查了学生对新定义的接受能力与转化能力,同时考查了单调性的定义,属于中档题.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
已知{an}是等比数列,若a6>0,则a6<a9是a6<a7的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
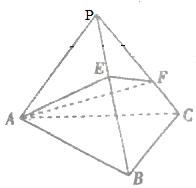 如图,在三棱锥P-ABC中,三个侧面都是顶角为20°的等腰三角形,侧棱长均为a,E、F分别是PB、PC上的点,则△AEF周长的最小值为( )
如图,在三棱锥P-ABC中,三个侧面都是顶角为20°的等腰三角形,侧棱长均为a,E、F分别是PB、PC上的点,则△AEF周长的最小值为( )