题目内容
在直角坐标系xOy中,曲线C1的参数方程是
,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C2的极坐标方程是ρsin(θ+
)=1,则两曲线交点间的距离是 .
|
| π |
| 6 |
考点:简单曲线的极坐标方程,参数方程化成普通方程
专题:坐标系和参数方程
分析:由曲线C1的参数方程是
,平方相减可得y2-x2=4.以坐曲线C2的极坐标方程是ρsin(θ+
)=1,展开为ρ(
sinθ+
cosθ)=1,化为y+
x=2.联立求出交点,再利用两点之间的距离公式即可得出.
|
| π |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
解答:
解:由曲线C1的参数方程是
,平方相减可得y2-x2=4.
以坐曲线C2的极坐标方程是ρsin(θ+
)=1,展开为ρ(
sinθ+
cosθ)=1,化为y+
x=2.
联立
,化为x2-2
x=0.解得x=0或2
.
∴
,
.
则两曲线交点间的距离是
=4
.
故答案为:4
.
|
以坐曲线C2的极坐标方程是ρsin(θ+
| π |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
联立
|
| 3 |
| 3 |
∴
|
|
则两曲线交点间的距离是
| 12+62 |
| 3 |
故答案为:4
| 3 |
点评:本题考查了把参数方程极坐标方程化为普通方程、直线与曲线的相交转化为方程联立可得交点坐标、两点之间的距离公式,考查了计算能力,属于基础题.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
函数f(x)=
的定义域为( )
| 1 | ||
|
| A、(0,3) |
| B、(0,3] |
| C、(3,+∞) |
| D、[3,+∞) |
已知点A在球O的表面上,过点A的作平面α,使OA与平面α成30°角,若平面α截球所得的圆面积为3π,则球O的体积为( )
A、
| ||
| B、4π | ||
C、
| ||
| D、16π |
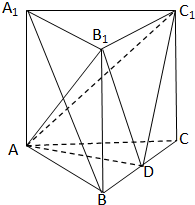 如图,三棱柱中ABC-A1B1C1,侧棱CC1⊥底面ABC,且侧棱和底面边长均为2,D是BC的中点
如图,三棱柱中ABC-A1B1C1,侧棱CC1⊥底面ABC,且侧棱和底面边长均为2,D是BC的中点