题目内容
loga（x+4）≤2x，x∈[0，1]恒成立，求a的取值范围．
考点：函数恒成立问题
专题：函数的性质及应用,不等式的解法及应用
分析：由x的范围求出2x的范围，然后分a＞1和0＜a＜1求出loga（x+4）的最大值，由loga（x+4）的最大值小于2x的最小值得a的取值范围．
解答：
解：当x∈[0，1]时，2x∈[1，2]，
x+4∈[4，5]，
当a＞1时，loga（x+4）的最大值为loga5，
由loga5≤1，得a≥5；
当0＜a＜1时，loga（x+4）的最大值为loga4，
由loga4≤1，得0＜a＜1．
综上，a的取值范围是（0，1）∪[5，+∞）．
x+4∈[4，5]，
当a＞1时，loga（x+4）的最大值为loga5，
由loga5≤1，得a≥5；
当0＜a＜1时，loga（x+4）的最大值为loga4，
由loga4≤1，得0＜a＜1．
综上，a的取值范围是（0，1）∪[5，+∞）．
点评：本题考查了函数恒成立问题，考查了指数函数和对数函数值域的求法，体现了数学转化思想方法，是中档题．
练习册系列答案
单元加期末复习先锋大考卷系列答案
出彩同步大试卷系列答案
相关题目
二次函数y=x2+bx与指数函数y=bx的图象只可能是（ ）
A、 |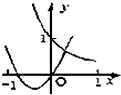
B、 |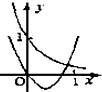
C、 |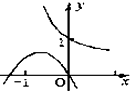
D、 |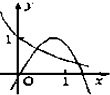
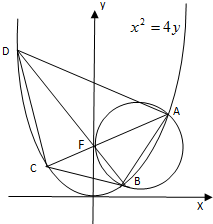已知抛物线G：x2=4y；
