题目内容
若在数列{an}中,a1=2,且2an+1+an=0(n∈N*),则an= .
考点:等比数列的通项公式
专题:等差数列与等比数列
分析:判断数列是等比数列,然后求出通项公式.
解答:
解:在数列{an}中,a1=2,且2an+1+an=0(n∈N*),
所以数列是公比为-
的等比数列.
所以an=a1(-
)n-1=2•(-
)n-1.
故答案为:2•(-
)n-1.
所以数列是公比为-
| 1 |
| 2 |
所以an=a1(-
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:2•(-
| 1 |
| 2 |
点评:本题考查等比数列的判断,通项公式的求法,基本知识的考查.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设方程sin4x=0的解集为M,方程cos2x=1的解集为P,则M与P之间的关系是( )
| A、P?M | B、M?P |
| C、M=P | D、M∩P=∅ |
函数f(x)的定义域为A,若存在非零实数t,使得对于任意x∈C(C⊆A)有x+t∈A,且f(x+t)≤f(x),则称f(x)为C上的t度低调函数.已知定义域为[0,+∞)的函数f(x)=-|mx-3|,且f(x)为[0,+∞)上的6度低调函数,那么实数m的取值范围是( )
| A、[0,1] |
| B、[1,+∞) |
| C、(-∞,0) |
| D、(-∞,0]∪[1,+∞) |
在△ABC中,D为边BC的中点,则下列向量关系式正确的是( )
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
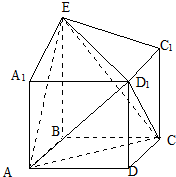 在如图所示的几何体中,底面ABCD为菱形,∠BAD=60°,AA1
在如图所示的几何体中,底面ABCD为菱形,∠BAD=60°,AA1