题目内容
数列{an}的前n项和为Sn,a1=1,an+1=2Sn+1(n≥1).
(1)求数列{an}的通项公式;
(2)等差数列{bn}的各项为正,b2=5,又a1+b1,a2+b2,a3+b3成等比数列,若cn=anbn,求Cn的前n项和Tn.
(1)求数列{an}的通项公式;
(2)等差数列{bn}的各项为正,b2=5,又a1+b1,a2+b2,a3+b3成等比数列,若cn=anbn,求Cn的前n项和Tn.
考点:数列的求和,数列递推式
专题:等差数列与等比数列
分析:(1)由an+1=2Sn+1可得an=2Sn-1+1(n≥2),相减得an+1-an=2an,an+1=3an(n≥2).即{an}是首项为1,公比为3的等比数列,问题得以解决.
(2)先求出数列{bn}的通项公式,把数列{an}和{bn}的通项公式代入cn=anbn,然后直接利用错位相减法求数列{cn}前n项和Tn,
(2)先求出数列{bn}的通项公式,把数列{an}和{bn}的通项公式代入cn=anbn,然后直接利用错位相减法求数列{cn}前n项和Tn,
解答:
解:(1)由an+1=2Sn+1可得an=2Sn-1+1(n≥2),
两式相减得an+1-an=2an,an+1=3an(n≥2).
又a2=2S1+1=3,∴a2=3a1.
故{an}是首项为1,公比为3的等比数列,
∴an=3n-1.
(2)设{bn}的公差为d,
由T3=15得b1+b2+b3=15,可得b2=5,
故可设b1=5-d,b3=5+d,
又a1=1,a2=3,a3=9,
由题意可得(5-d+1)(5+d+9)=(5+3)2,
解得d1=2,d2=-10.
∵等差数列{bn}的各项为正,
∴d>0.
∴d=2,b1=3
∴bn=2n+1,
∴Cn=(2n+1)•3n-1.
∴Tn=3×30+5×31+7×32+…+(2n+1)×3n-1 ①,
3Tn=3×31+5×32+7×33+…+(2n+1)×3n ②,
①-②得:-2Tn=3+2×31+2×32+2×33+…+2×3n-1-(2n+1)×3n=3-(2n+1)×3n+2×
=3-(2n+1)×3n-3+3n=-2n×3n
∴Tn=n×3n
两式相减得an+1-an=2an,an+1=3an(n≥2).
又a2=2S1+1=3,∴a2=3a1.
故{an}是首项为1,公比为3的等比数列,
∴an=3n-1.
(2)设{bn}的公差为d,
由T3=15得b1+b2+b3=15,可得b2=5,
故可设b1=5-d,b3=5+d,
又a1=1,a2=3,a3=9,
由题意可得(5-d+1)(5+d+9)=(5+3)2,
解得d1=2,d2=-10.
∵等差数列{bn}的各项为正,
∴d>0.
∴d=2,b1=3
∴bn=2n+1,
∴Cn=(2n+1)•3n-1.
∴Tn=3×30+5×31+7×32+…+(2n+1)×3n-1 ①,
3Tn=3×31+5×32+7×33+…+(2n+1)×3n ②,
①-②得:-2Tn=3+2×31+2×32+2×33+…+2×3n-1-(2n+1)×3n=3-(2n+1)×3n+2×
| 3(1-3n-1) |
| 1-3 |
∴Tn=n×3n
点评:本题考查了等差数列和等比数列的通项公式,考查了错位相减法求数列的和,是中档题.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
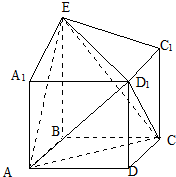 在如图所示的几何体中,底面ABCD为菱形,∠BAD=60°,AA1
在如图所示的几何体中,底面ABCD为菱形,∠BAD=60°,AA1