题目内容
已知f(x)=
为偶函数,则y=loga(x2-4x-5)的单调递增区间为( )
|
| A、(-∞,-1) |
| B、(-∞,2) |
| C、(2,+∞) |
| D、(5,+∞) |
考点:复合函数的单调性,函数奇偶性的判断
专题:函数的性质及应用
分析:首先根据偶函数的性质求才a=2,然后根据复合函数的内外同增则增的原则,因为y=log2t是定义域上的递增函数,只要求t=x2-4x-5的递增区间即可,但要注意定义域.
解答:
解:∵f(x)=
为偶函数,∴f(-1)=f(1),∴1-a=1-2,∴a=2
则函数y=loga(x2-4x-5)即y=log2(x2-4x-5),令t=x2-4x-5,x=2是对称轴
由x2-4x-5>0,得x<-1或x>5,由复合函数的单调性,知(5,+∞)是所求函数
的递增区间.
故答案选:D
|
则函数y=loga(x2-4x-5)即y=log2(x2-4x-5),令t=x2-4x-5,x=2是对称轴
由x2-4x-5>0,得x<-1或x>5,由复合函数的单调性,知(5,+∞)是所求函数
的递增区间.
故答案选:D
点评:本题考查复合函数的单调区间,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
函数y=x2+2x的减区间是( )
| A、(-∞,-1] |
| B、[-1,+∞) |
| C、(-∞,0] |
| D、(-∞,+∞) |
300°转化为弧度是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
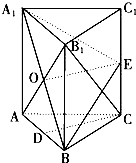 如图三棱柱ABC-A1B1C1中,每个侧面都是正方形,D为底边AB中点,E为侧棱CC1中点,AB1与A1B交于点O.
如图三棱柱ABC-A1B1C1中,每个侧面都是正方形,D为底边AB中点,E为侧棱CC1中点,AB1与A1B交于点O.