题目内容
直线L1:y=x,与直线L2:y=kx(k>0),点P(m,m)是L1上的动点,以P为圆心的圆切直线L2于点A,过点P作垂直于x轴的直线交L2于B.
(1)当|OB|=5|BA|时,求直线L2的方程;
(2)若圆P的半径为1,△OPA的面积为1,求L2的方程.
(1)当|OB|=5|BA|时,求直线L2的方程;
(2)若圆P的半径为1,△OPA的面积为1,求L2的方程.
考点:直线和圆的方程的应用
专题:综合题,直线与圆
分析:(1)设A(x,y),B(m,km),则由|OB|=5|BA|,可得
=
或
=
,求出A的坐标,利用直线OA与AP垂直,建立方程,即可求直线L2的方程;
(2)利用圆P的半径为1,△OPA的面积为1,求出P的坐标,利用点到直线的距离等于半径,即可求L2的方程.
| OA |
| 1 |
| 4 |
| OB |
| OA |
| 6 |
| 5 |
| OB |
(2)利用圆P的半径为1,△OPA的面积为1,求出P的坐标,利用点到直线的距离等于半径,即可求L2的方程.
解答:
解:(1)设A(x,y),B(m,km),则
∵|OB|=5|BA|,∴
=
或
=
.
=
时,由(x,y)=
(m,km),可得A(
,
),∴k•
=-1,∴k=-2(舍去);
=
时,由(x,y)=
(m,km),可得A(
,
),∴k•
=-1,∴k=
,
∴直线L2的方程为y=
x;
(2)∵圆P的半径为1,△OPA的面积为1,
∴|OA|=2,|OP|=
,
∴P(
,
),
∴
=1,
∴3k2-10k+3=0,
∴k=3或k=
,
∴直线L2的方程为y=3x或y=
x.
∵|OB|=5|BA|,∴
| OA |
| 1 |
| 4 |
| OB |
| OA |
| 6 |
| 5 |
| OB |
| OA |
| 1 |
| 4 |
| OB |
| 1 |
| 4 |
| m |
| 4 |
| km |
| 4 |
m-
| ||
m-
|
| OA |
| 6 |
| 5 |
| OB |
| 6 |
| 5 |
| 6m |
| 5 |
| 6km |
| 5 |
| ||
|
| 5 |
| 7 |
∴直线L2的方程为y=
| 5 |
| 7 |
(2)∵圆P的半径为1,△OPA的面积为1,
∴|OA|=2,|OP|=
| 5 |
∴P(
| ||
| 2 |
| ||
| 2 |
∴
|
| ||||||||
|
∴3k2-10k+3=0,
∴k=3或k=
| 1 |
| 3 |
∴直线L2的方程为y=3x或y=
| 1 |
| 3 |
点评:本题考查直线方程,考查直线与圆的位置关系,考查点到直线的距离公式,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
已知集合P={x,y,z},Q={1,2,3},映射f:P→Q中满足f(y)=2的映射的个数共有( )
| A、2 | B、4 | C、6 | D、9 |
以O为中心,F1,F2为两个焦点的椭圆上存在一点M,满足|
|=2|
|=2|
|,则该椭圆的离心率为( )
| MF1 |
| MO |
| MF2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
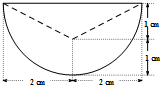 某零件的正(主)视图与侧(左)视图均是如图所示的图形(实线组成半径为2cm的半圆,虚线是等腰三角形的两腰),俯视图是一个半径为2cm的圆(包括圆心),则该零件的体积是
某零件的正(主)视图与侧(左)视图均是如图所示的图形(实线组成半径为2cm的半圆,虚线是等腰三角形的两腰),俯视图是一个半径为2cm的圆(包括圆心),则该零件的体积是