题目内容
若曲线y=ln2x在点P处的切线斜率为1,则点P的坐标为 .
考点:利用导数研究曲线上某点切线方程
专题:计算题,导数的概念及应用
分析:利用曲线y=ln2x在点P处的切线斜率为1,结合导数的几何意义,即可求出切点的坐标.
解答:
解:由y=ln2x可得y′=
令y′=
=1,可得x=
代入y=ln2x,可得y=0,
∴切点坐标为(
,0).
故答案为:(
,0).
| 1 |
| x |
令y′=
| 1 |
| x |
| 1 |
| 2 |
代入y=ln2x,可得y=0,
∴切点坐标为(
| 1 |
| 2 |
故答案为:(
| 1 |
| 2 |
点评:本题考查导数的几何意义,考查曲线的切线,考查学生的计算能力,属于基础题.

练习册系列答案
相关题目
下列表示方法正确的是( )
| A、0∈∅ | B、∅∈{0} |
| C、∅∉{0} | D、0∈{O} |
 根据如图程序,当输入a的值为3,b的值为-5时,输出值:a=
根据如图程序,当输入a的值为3,b的值为-5时,输出值:a=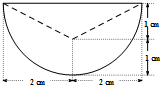 某零件的正(主)视图与侧(左)视图均是如图所示的图形(实线组成半径为2cm的半圆,虚线是等腰三角形的两腰),俯视图是一个半径为2cm的圆(包括圆心),则该零件的体积是
某零件的正(主)视图与侧(左)视图均是如图所示的图形(实线组成半径为2cm的半圆,虚线是等腰三角形的两腰),俯视图是一个半径为2cm的圆(包括圆心),则该零件的体积是