题目内容
已知双曲线
-
=1的左焦点为F1,点P为双曲线右支上一点,且PF1与圆x2+y2=16相切于点N,M为线段PF1的中点,O为坐标原点,则|MN|-|MO|的值为( )
| x2 |
| 16 |
| y2 |
| 25 |
| A、2 | B、-1 | C、1 | D、-2 |
考点:双曲线的简单性质
专题:综合题,圆锥曲线的定义、性质与方程
分析:依题意,作出图形,点P在双曲线右支上,利用双曲线的定义,可知,|PF1|-|PF2|=2a=8,|MF1|-|OM|=
|PF1|-
|PF2|=4,转化后计算可得|MN|-|OM|=1,从而得到答案.
| 1 |
| 2 |
| 1 |
| 2 |
解答:
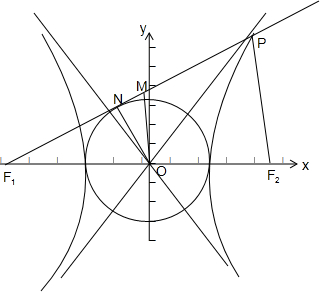 解:依题意,作图如图:
解:依题意,作图如图:
由双曲线方程
-
=1知,a2=16,b2=25,
∴c2=a2+b2=16+25=41,
依题意知,|PF1|-|PF2|=2a=8,
∵点M为线段PF1的中点,O为F1F2的中点,
∴|OM|=
|PF2|,|MF1|=
|PF1|,
∴|MF1|-|OM|=
|PF1|-
|PF2|=4,①
又在直角△NF1O中,|ON|=4,|OF1|=c=
,
∴|NF1|=
=5,②
而|MF1|-|NF1|=|MN|,
∴|MN|+5-|OM|=4.
∴|MN|-|OM|=4-5=-1.
故选:B.
 解:依题意,作图如图:
解:依题意,作图如图:由双曲线方程
| x2 |
| 16 |
| y2 |
| 25 |
∴c2=a2+b2=16+25=41,
依题意知,|PF1|-|PF2|=2a=8,
∵点M为线段PF1的中点,O为F1F2的中点,
∴|OM|=
| 1 |
| 2 |
| 1 |
| 2 |
∴|MF1|-|OM|=
| 1 |
| 2 |
| 1 |
| 2 |
又在直角△NF1O中,|ON|=4,|OF1|=c=
| 41 |
∴|NF1|=
(
|
而|MF1|-|NF1|=|MN|,
∴|MN|+5-|OM|=4.
∴|MN|-|OM|=4-5=-1.
故选:B.
点评:本题考查双曲线的定义,考查三角形的中位线定理与勾股定理的应用,考查分析转化思想与运算求解能力,属于难题.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
下列表示方法正确的是( )
| A、0∈∅ | B、∅∈{0} |
| C、∅∉{0} | D、0∈{O} |
以O为中心,F1,F2为两个焦点的椭圆上存在一点M,满足|
|=2|
|=2|
|,则该椭圆的离心率为( )
| MF1 |
| MO |
| MF2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
某几何体的三视图如图所示,则此几何体的体积是( )


| A、2+3π | B、3+3π |
| C、4+3π | D、5+3π |
已知全集U={1,2,3,4,5},A={2,4,5},则∁uA=( )
| A、∅ |
| B、{1,2,4} |
| C、{2,4,5} |
| D、{1,3} |
在区间[-2π,2π]范围内,函数y=tanx与函数y=sinx的图象交点的个数为( )
| A、3 | B、5 | C、7 | D、9 |
y=sinx+
cosx(0≤x≤
),则y的最小值为( )
| 3 |
| π |
| 2 |
| A、-2 | ||
| B、-1 | ||
| C、1 | ||
D、
|
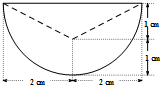 某零件的正(主)视图与侧(左)视图均是如图所示的图形(实线组成半径为2cm的半圆,虚线是等腰三角形的两腰),俯视图是一个半径为2cm的圆(包括圆心),则该零件的体积是
某零件的正(主)视图与侧(左)视图均是如图所示的图形(实线组成半径为2cm的半圆,虚线是等腰三角形的两腰),俯视图是一个半径为2cm的圆(包括圆心),则该零件的体积是