题目内容
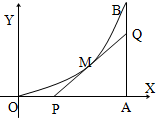 如图,由y=0,x=8,y=x2围城的曲边三角形,在曲线OB弧上求一点M,使得过M所作的y=x2的切线PQ与OA,AB围城的三角形PQA的面积最大.
如图,由y=0,x=8,y=x2围城的曲边三角形,在曲线OB弧上求一点M,使得过M所作的y=x2的切线PQ与OA,AB围城的三角形PQA的面积最大.考点:利用导数研究曲线上某点切线方程
专题:计算题,导数的综合应用
分析:设 M(x0,y0),PQ:y=k(x-x0)+y0,求出y=x2的导数,求出切线的斜率,令x=8,y=0求得P,Q的坐标,
再求出三角形PQA的面积,再由导数求出最大值.
再求出三角形PQA的面积,再由导数求出最大值.
解答:
解:设 M(x0,y0),PQ:y=k(x-x0)+y0
则 y0=
,y′=2x|x=x0=2x0
即k=2x0所以y=2x0(x-x0)+y0
令y=0则x=x0-
=
x0,
即P(
,0)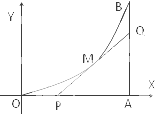
令x=8则y=16x0-
Q(8,16x0-
)
S=S△PAQ=
(8-
)(16x0-
)
=64x0-8
+
S′=64-16x0+
令S'=0,则x0=16(舍去)或x0=
,
在
处S'左正右负,即为极大值点,也是最大值点.
即当x0=
时,Smax=
此时y0=(
)2=
M(
,
).
则 y0=
| x | 2 0 |
即k=2x0所以y=2x0(x-x0)+y0
令y=0则x=x0-
| y0 |
| 2x0 |
| 1 |
| 2 |
即P(
| x0 |
| 2 |

令x=8则y=16x0-
| x | 2 0 |
Q(8,16x0-
| x | 2 0 |
S=S△PAQ=
| 1 |
| 2 |
| x0 |
| 2 |
| x | 2 0 |
=64x0-8
| x | 2 0 |
| 1 |
| 4 |
| x | 3 0 |
S′=64-16x0+
| 3 |
| 4 |
| x | 2 0 |
令S'=0,则x0=16(舍去)或x0=
| 16 |
| 3 |
在
| 16 |
| 3 |
即当x0=
| 16 |
| 3 |
| 4096 |
| 27 |
此时y0=(
| 16 |
| 3 |
| 256 |
| 9 |
M(
| 16 |
| 3 |
| 256 |
| 9 |
点评:本题考查导数的几何意义,运用导数求切线方程,求最值,考查运算能力,是一道中档题.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
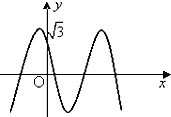 如图,函数f(x)=2cos(ωx+θ)(x∈R,ω>0,0≤θ≤
如图,函数f(x)=2cos(ωx+θ)(x∈R,ω>0,0≤θ≤ 如图,已知定点F(-1,0),N(1,0),以线段FN为对角线作周长是8的平行四边形MNEF.
如图,已知定点F(-1,0),N(1,0),以线段FN为对角线作周长是8的平行四边形MNEF.