题目内容
已知函数f(x)=
,求f(x)的单调区间.
| -x2+3x+10 |
考点:复合函数的单调性
专题:函数的性质及应用
分析:由-x2+3x+10≥0先求出原函数的定义域,然后令t=-x2+3x+10,则y=
,再按照“同增异减”的原则在定义域内求出原函数的单调期间.
| t |
解答:
解:由-x2+3x+10≥0解得-2≤x≤5,
所以原函数的定义域为[-2,5],
令t=-x2+3x+10,则y=
,
对于二次函数t=-x2+3x+10,其图象开口向下,对称轴x=
,
借助图象可知,其在[-2,
]上递增,在(
,5]递减,
因此,当x∈[-2,
]时,t随着x的增大而增大,则y=
也跟着增大,所以函数y=
在[-2,
]上单调递增;
同理,当x∈(
,5]时,t随着x的增大而减小,则y=
也跟着减小,所以函数y=
在(
,5]上单调递减.
所以原函数的单调递增区间为[-2,
],递减区间为(
,5].
所以原函数的定义域为[-2,5],
令t=-x2+3x+10,则y=
| t |
对于二次函数t=-x2+3x+10,其图象开口向下,对称轴x=
| 3 |
| 2 |
借助图象可知,其在[-2,
| 3 |
| 2 |
| 3 |
| 2 |
因此,当x∈[-2,
| 3 |
| 2 |
| t |
| -x2+3x+10 |
| 3 |
| 2 |
同理,当x∈(
| 3 |
| 2 |
| t |
| -x2+3x+10 |
| 3 |
| 2 |
所以原函数的单调递增区间为[-2,
| 3 |
| 2 |
| 3 |
| 2 |
点评:对于此类问题,首先强调定义域优先的原则,此例研究了求复合函数的单调性的方法,遵循“同增异减”的原则,关键是弄清内外函数单调性,再进行求解.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
将函数f(x)=sin(ωx+
)的图象关于x=
对称,则ω的值可能是( )
| π |
| 6 |
| π |
| 6 |
A、
| ||
B、
| ||
| C、5 | ||
| D、2 |
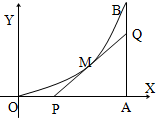 如图,由y=0,x=8,y=x2围城的曲边三角形,在曲线OB弧上求一点M,使得过M所作的y=x2的切线PQ与OA,AB围城的三角形PQA的面积最大.
如图,由y=0,x=8,y=x2围城的曲边三角形,在曲线OB弧上求一点M,使得过M所作的y=x2的切线PQ与OA,AB围城的三角形PQA的面积最大.