题目内容
函数f（x）=sinx在x=π处的切线方程为 ．
考点：利用导数研究曲线上某点切线方程
专题：导数的综合应用
分析：求出原函数的导函数，得到函数在x=π处的导数值，再求得f（π），由直线方程的点斜式得答案．
解答：
解：由f（x）=sinx，得
f′（x）=cosx，
∴f′（π）=-1．
又f（π）=sinπ=0．
∴函数f（x）=sinx在x=π处的切线方程为y=-1×（x-π）．
即y=-x+π．
故答案为：y=-x+π．
f′（x）=cosx，
∴f′（π）=-1．
又f（π）=sinπ=0．
∴函数f（x）=sinx在x=π处的切线方程为y=-1×（x-π）．
即y=-x+π．
故答案为：y=-x+π．
点评：本题考查了利用导数研究过曲线上某点处的切线方程，过曲线上某点的切线的斜率，就是函数在该点处的导数值，是中档题．
练习册系列答案
相关题目
如图，在三棱柱ABC-A1B1C1中，AA1⊥平面ABC，D、E、F分别是AB、BB1、CC1的中点，AB=BC=AC=BB1=2．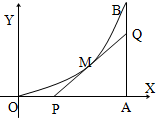
如图，由y=0，x=8，y=x2围城的曲边三角形，在曲线OB弧上求一点M，使得过M所作的y=x2的切线PQ与OA，AB围城的三角形PQA的面积最大．
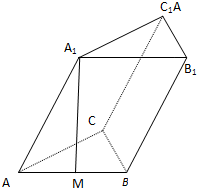已知斜三棱柱ABC-A1B1C1的底面是正三角形，侧面ABB1A1是菱形，且∠A1AB=60°，M是AB的中点，A1M⊥AC