题目内容
已知函数f（x）=|x|+
，判断并证明函数f（x）的奇偶性．
| x2 |
考点：函数奇偶性的判断
专题：函数的性质及应用
分析：根据函数奇偶性的定义，即可得到结论．
解答：
解：函数的定义域为R，
则f（-x）=|x|+
=f（x），
故函数是偶函数．
则f（-x）=|x|+
| x2 |
故函数是偶函数．
点评：本题主要考查函数奇偶性的判断，根据奇偶性的定义是解决本题的关键．
练习册系列答案
相关题目
如图，在三棱柱ABC-A1B1C1中，AA1⊥平面ABC，D、E、F分别是AB、BB1、CC1的中点，AB=BC=AC=BB1=2．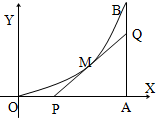
如图，由y=0，x=8，y=x2围城的曲边三角形，在曲线OB弧上求一点M，使得过M所作的y=x2的切线PQ与OA，AB围城的三角形PQA的面积最大．