题目内容
已知椭圆
+
=1上一点到椭圆两焦点的距离之和为4
.
(Ⅰ)求a的值及椭圆的离心率;
(Ⅱ)顺次连结椭圆的顶点得到菱形A1B1A2B2,求该菱形的内切圆方程;
(Ⅲ)直线l与(Ⅱ)中的圆相切并交椭圆于A,B两点,求|AB|的取值范围.
| x2 |
| a2 |
| y2 |
| 4 |
| 2 |
(Ⅰ)求a的值及椭圆的离心率;
(Ⅱ)顺次连结椭圆的顶点得到菱形A1B1A2B2,求该菱形的内切圆方程;
(Ⅲ)直线l与(Ⅱ)中的圆相切并交椭圆于A,B两点,求|AB|的取值范围.
考点:圆锥曲线的实际背景及作用,两点间的距离公式,圆的标准方程,椭圆的简单性质
专题:综合题,圆锥曲线的定义、性质与方程
分析:(Ⅰ)椭圆上的点到椭圆两焦点的距离之和为4
,可求a的值,求出c,即可求出椭圆的离心率;
(Ⅱ)顺次连结椭圆的顶点得到菱形A1B1A2B2,求出内切圆的圆心,即可求该菱形的内切圆方程;
(Ⅲ)分类讨论,设直线方程代入椭圆方程,利用弦长公式,即可求|AB|的取值范围.
| 2 |
(Ⅱ)顺次连结椭圆的顶点得到菱形A1B1A2B2,求出内切圆的圆心,即可求该菱形的内切圆方程;
(Ⅲ)分类讨论,设直线方程代入椭圆方程,利用弦长公式,即可求|AB|的取值范围.
解答:
解:(Ⅰ)∵椭圆上的点到椭圆两焦点的距离之和为4
,
∴2a=4
,∴a=2
,
∵b=2,∴c=2,
∴e=
=
;
(Ⅱ)∵a=2
,b=2,
∴菱形内切圆的半径r=
=
∴内切圆方程为x2+y2=
(Ⅲ)①当直线斜率不存在时,直线方程为x=±
代入椭圆方程得y=±
此时|AB|=
②当直线斜率为0时,直线方程为y=±
代入椭圆方程得x=±
此时|AB|=
③当直线的斜率存在且不为0时,设直线方程为y=kx+m
由直线与圆相切得
=
,即m2=
(1+k2)
直线代入椭圆方程,可得(1+2k2)x2+4kmx+2m2-8=0,
设A ( x1,y1 ),B (x2,y2 ),
则x1+x2=-
,x1x2=
,
|AB|=
|x1-x2|
≤2
,
∴|AB|∈[
,2
].
| 2 |
∴2a=4
| 2 |
| 2 |
∵b=2,∴c=2,
∴e=
| c |
| a |
| ||
| 2 |
(Ⅱ)∵a=2
| 2 |
∴菱形内切圆的半径r=
2×2
| ||
2
|
2
| ||
| 3 |
∴内切圆方程为x2+y2=
| 8 |
| 3 |
(Ⅲ)①当直线斜率不存在时,直线方程为x=±
2
| ||
| 3 |
2
| ||
| 3 |
此时|AB|=
4
| ||
| 3 |
②当直线斜率为0时,直线方程为y=±
2
| ||
| 3 |
2
| ||
| 3 |
此时|AB|=
4
| ||
| 3 |
③当直线的斜率存在且不为0时,设直线方程为y=kx+m
由直线与圆相切得
| |m| | ||
|
2
| ||
| 3 |
| 8 |
| 3 |
直线代入椭圆方程,可得(1+2k2)x2+4kmx+2m2-8=0,
设A ( x1,y1 ),B (x2,y2 ),
则x1+x2=-
| 4km |
| 1+2k2 |
| 2m2-8 |
| 1+2k2 |
|AB|=
| 1+k2 |
|
| 3 |
∴|AB|∈[
4
| ||
| 3 |
| 3 |
点评:本题考查椭圆的方程与性质,考查直线与椭圆的位置关系,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
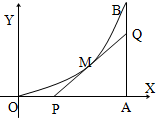 如图,由y=0,x=8,y=x2围城的曲边三角形,在曲线OB弧上求一点M,使得过M所作的y=x2的切线PQ与OA,AB围城的三角形PQA的面积最大.
如图,由y=0,x=8,y=x2围城的曲边三角形,在曲线OB弧上求一点M,使得过M所作的y=x2的切线PQ与OA,AB围城的三角形PQA的面积最大.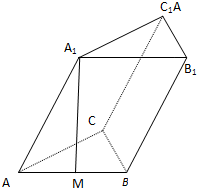 已知斜三棱柱ABC-A1B1C1的底面是正三角形,侧面ABB1A1是菱形,且∠A1AB=60°,M是AB的中点,A1M⊥AC
已知斜三棱柱ABC-A1B1C1的底面是正三角形,侧面ABB1A1是菱形,且∠A1AB=60°,M是AB的中点,A1M⊥AC