题目内容
 如图,已知定点F(-1,0),N(1,0),以线段FN为对角线作周长是8的平行四边形MNEF.
如图,已知定点F(-1,0),N(1,0),以线段FN为对角线作周长是8的平行四边形MNEF.(Ⅰ)求点E、M所在曲线C的方程;
(Ⅱ)过点N的直线l:x=my+1与曲线C交于P,Q两点,则△FPQ的内切圆的面积是否存在最大值?若存在,求出这个最大值及直线l的方程;若不存在,请说明理由.
考点:直线与圆锥曲线的综合问题,轨迹方程
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)由已知得|EF|+|EN|=4》2=|FN|,曲线C的轨迹为椭圆(去掉左右顶点),由此能求出点E、M所在曲线C的方程.
(2)设P(x1,y1),Q(x2,y2),设y1>0,y2<0,△FPQ的内切圆半径为R,则S△FPQ=
(|PQ|+|PF|+|QF|)R=
×4a×R=4R,当S△EFQ最大时,R也最大,△FPQ的内切圆的面积也最大,S△FPQ=
•|FN|•|y1-y2|=|y1-y2|,由
,得(3m2+4)y2+6my-9=0,由此利用弦长公式、导数性质能求出△FPQ的内切圆的最大值和直线l的方程.
(2)设P(x1,y1),Q(x2,y2),设y1>0,y2<0,△FPQ的内切圆半径为R,则S△FPQ=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
|
解答:
解:(Ⅰ)∵四边形MNEF是周长为8的平行四边形,
∴|EF|+|EN|=4》2=|FN|,
由椭圆定义知,曲线C的轨迹为椭圆(去掉左右顶点),
且2a=4,2c=2,∴b2=a2-c2=3,
∴点E、M所在曲线C的方程为
+
=1,y≠0.
(2)设P(x1,y1),Q(x2,y2),不妨设y1>0,y2<0,
设△FPQ的内切圆半径为R,
则S△FPQ=
(|PQ|+|PF|+|QF|)R=
×4a×R=4R,
当S△EFQ最大时,R也最大,△FPQ的内切圆的面积也最大,
又S△FPQ=
•|FN|•|y1-y2|=|y1-y2|,
由
,得(3m2+4)y2+6my-9=0,
△=(6m)2+4×9(3m2+4)>0恒成立,
y1+y2=
,y1y2=
,
|y1-y2|=
=
=
,
∴S△FPQ=
,
设
=t,则f′(t)=
,
∵t≥1,∴f′(t)<0,
∴函数f(t)在[1,+∞)上是单调减函数,
∴f(t)max=f(1)=3,
即S△FPQ的最大值是3,
又S△FPQ=4R,∴R=
,m=0,
∴△FPQ的内切圆的最大值为
,直线l的方程为x=1.
∴|EF|+|EN|=4》2=|FN|,
由椭圆定义知,曲线C的轨迹为椭圆(去掉左右顶点),
且2a=4,2c=2,∴b2=a2-c2=3,
∴点E、M所在曲线C的方程为
| x2 |
| 4 |
| y2 |
| 3 |
(2)设P(x1,y1),Q(x2,y2),不妨设y1>0,y2<0,
设△FPQ的内切圆半径为R,
则S△FPQ=
| 1 |
| 2 |
| 1 |
| 2 |
当S△EFQ最大时,R也最大,△FPQ的内切圆的面积也最大,
又S△FPQ=
| 1 |
| 2 |
由
|
△=(6m)2+4×9(3m2+4)>0恒成立,
y1+y2=
| -6m |
| 3m2+4 |
| -9 |
| 3m2+4 |
|y1-y2|=
| (y1+y2)2-4y1y2 |
=
(
|
=
12
| ||
| 3m2+4 |
∴S△FPQ=
12
| ||
| 3m2+4 |
设
| m2+1 |
| 12-36t2 |
| (3t2+1)2 |
∵t≥1,∴f′(t)<0,
∴函数f(t)在[1,+∞)上是单调减函数,
∴f(t)max=f(1)=3,
即S△FPQ的最大值是3,
又S△FPQ=4R,∴R=
| 3 |
| 4 |
∴△FPQ的内切圆的最大值为
| 9π |
| 16 |
点评:本题考查曲线方程的求法,考查三角形内切圆面积的最大值的求法,考查直线方程的求法,解题时要认真审题,注意弦长公式、导数性质的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
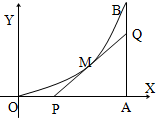 如图,由y=0,x=8,y=x2围城的曲边三角形,在曲线OB弧上求一点M,使得过M所作的y=x2的切线PQ与OA,AB围城的三角形PQA的面积最大.
如图,由y=0,x=8,y=x2围城的曲边三角形,在曲线OB弧上求一点M,使得过M所作的y=x2的切线PQ与OA,AB围城的三角形PQA的面积最大.