题目内容
已知命题p:|1+
|≤2;命题q:x2+2x+1-m2≤0(m>0).若?p是?q的必要而不充分条件,则实数m的取值范围为 .
| x-1 |
| 3 |
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:把充分性问题,转化为集合的关系求解.
解答:
解:∵命题p:|1+
|≤2;命题q:x2+2x+1-m2≤0(m>0).
∴p:-8≤x≤4,q:x2+2x+1-m2≤0(m>0).
∴?p是?q的必要而不充分条件,
即p是q的充分不必要条件,
,可以知集合p是集合q的真子集,
∴
,即
又m>0,∴m≥7
故答案为:[7,+∞)
| x-1 |
| 3 |
∴p:-8≤x≤4,q:x2+2x+1-m2≤0(m>0).
∴?p是?q的必要而不充分条件,
即p是q的充分不必要条件,
,可以知集合p是集合q的真子集,
∴
|
|
又m>0,∴m≥7
故答案为:[7,+∞)
点评:本题考查了不等式与简易逻辑知识,难度不大.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案
相关题目
若函数f(x)=Asin2ωx(A>0,ω>0)在x=1处取得最大值,则f(x+1)的奇偶性为( )
| A、偶函数 |
| B、奇函数 |
| C、既是奇函数又是偶函数 |
| D、非奇非偶函数 |
为了得到函数f(x)=cos(2x+
)的图象,只要把函数g(x)=
f′(x)的图象( )
| π |
| 4 |
| 1 |
| 2 |
A、向左平行移动
| ||
B、向右平行移动
| ||
C、向左平行移动
| ||
D、向右平行移动
|
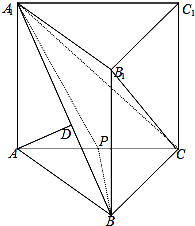 如图,直三棱柱ABC-A1B1C1中,AD⊥平面A1BC,其垂足D落在直线A1B上.P为AC的中点.
如图,直三棱柱ABC-A1B1C1中,AD⊥平面A1BC,其垂足D落在直线A1B上.P为AC的中点.