题目内容
已知
=
,求cos4(
+α)-cos4(
-α).
| sinα-cosα |
| sinα+cosα |
| 1 |
| 3 |
| π |
| 3 |
| π |
| 6 |
考点:三角函数的化简求值
专题:三角函数的求值
分析:根据三角函数的诱导公式进行化简即可.
解答:
解:cos4(
+α)-cos4(
-α)=cos4(
+α)-sin4(
+α)=[cos2(
+α)+sin2(
+α)][cos2(
+α)-sin2(
+α)]
=cos2(
+α)-sin2(
+α)=cos(
+2α)=2cos2(
+α)-1.
由
=
,得sinα=2cosα,解得cosα=
,sinα=
,或cos=-
,sinα=-
,
若cosα=
,sinα=
,则cos(
+α)=cos
cosα-sin
sinα=
×
-
×
=
,
若cos=-
,sinα=-
,则cos(
+α)=cos
cosα-sin
sinα=-
×
-
×(-
)=-
,
则2cos2(
+α)-1=2(±
)2-1=
.
| π |
| 3 |
| π |
| 6 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
=cos2(
| π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
| π |
| 3 |
由
| sinα-cosα |
| sinα+cosα |
| 1 |
| 3 |
| ||
| 5 |
2
| ||
| 5 |
| ||
| 5 |
2
| ||
| 5 |
若cosα=
| ||
| 5 |
2
| ||
| 5 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| 1 |
| 2 |
| ||
| 5 |
| ||
| 2 |
2
| ||
| 5 |
| ||||
| 10 |
若cos=-
| ||
| 5 |
2
| ||
| 5 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| 1 |
| 2 |
| ||
| 5 |
| ||
| 2 |
2
| ||
| 5 |
| ||||
| 10 |
则2cos2(
| π |
| 3 |
| ||||
| 10 |
1-2
| ||
| 5 |
点评:本题主要考查三角函数值的化简和求解,利用余弦函数的倍角公式已经两角和差的余弦公式是解决本题的关键.

练习册系列答案
相关题目
点(x,y)的坐标x,y都是有理数时,该点称为有理点,在半径为r,圆心为(a,b)的圆中,若a∈Q,b∈Q,则这个圆上的有理点的数目为( )
| A、最多有一个 |
| B、最多有两个 |
| C、最多有三个 |
| D、可以有无穷多个 |
要得到函数y=cos(2x+
)的图象,只需将函数y=cos2x的图象( )
| π |
| 3 |
A、向左平移
| ||
B、向左平移
| ||
C、向右平移
| ||
D、向右平移
|
若直线l经过点A(1,2),B(4,2+
),则直线l的倾斜角是( )
| 3 |
| A、30° | B、45° |
| C、60° | D、90° |
命题:“对任意的x∈R,x3-x2+1≤0”的否定是( )
| A、不存在x∈R,x3-x2+1≤0 |
| B、存在x0∈R,x03-x02+1>0 |
| C、存在x0∈R,x03-x02+1≤0 |
| D、对任意的x∈R,x3-x2+1>0 |
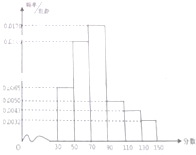 某县为“中学生知识竞赛”进行选取性测试,规定:成绩大于或等于90分的右参赛资格,90分以下(不包括90分)的则被淘汰,若现有1000人参加测试,学生成绩的频率分别直方图如图:
某县为“中学生知识竞赛”进行选取性测试,规定:成绩大于或等于90分的右参赛资格,90分以下(不包括90分)的则被淘汰,若现有1000人参加测试,学生成绩的频率分别直方图如图: