题目内容
化简:sin2242°+tan2(-64°)cot45°•
+cos2782°.
| 1 |
| tan2244° |
考点:三角函数的化简求值
专题:三角函数的求值
分析:利用三角函数的诱导公式进行化简即可.
解答:
解:原式=sin262°+tan2(64°)×1•
+cos2(720°+62°)=sin262°+1+cos262°=1+1=2.
| 1 |
| tan264° |
点评:本题主要考查三角函数值的化简和求值,利用三角函数的诱导公式以及同角的关系式是解决本题的关键.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
函数f(x)=xln|x|的大致图象是( )
A、 |
B、 |
C、 |
D、 |
下列说法中,正确的是( )
| A、数据5,4,4,3,5,2,1的中位数是3 |
| B、一组数据的标准差是这组数据的方差的平方 |
| C、频率分布直方图中各小长方形的面积等于相应各组的频数 |
| D、数据2,3,4,5 的标准差是数据4,6,8,10的标准差的一半 |
化简:tan(18°-x)tan(12°+x)+
[tan(18°-x)+tan(12°+x)]得( )
| 3 |
| A、0 | ||||
| B、1 | ||||
C、
| ||||
D、
|
已知函数y=f(x),x∈R,则f′(x0)表示( )
| A、自变量x=x0时对应的函数值 |
| B、函数值y在x=x0时的瞬时变化率 |
| C、函数值y在x=x0时的平均变化率 |
| D、无意义 |
已知a=3
,b=log3
,c=log
,则( )
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| A、a>b>c |
| B、a>c>b |
| C、c>a>b |
| D、c>b>a |
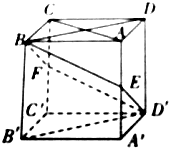 如图,在正方体ABCD-A′B′C′D′中,E,F分别是A′A,C′C的中点,则下列判断中正确的是
如图,在正方体ABCD-A′B′C′D′中,E,F分别是A′A,C′C的中点,则下列判断中正确的是