题目内容
14.设等比数列{an}的前n项和为Sn,已知a1=2,且4S1,3S2,2S3成等差数列.(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn=|2n-5|•an,求数列{bn}的前n项和Tn.
分析 (Ⅰ)根据4S1,3S2,2S3成等差数列.根据等差中项6S2=4S1+2S3,化简整理求得q=2,写出通项公式;
(Ⅱ)讨论当n=1、2时,求得T1=6,T2=10,写出前n项和,采用错位相减法求得Tn.
解答 解:(Ⅰ)∵4S1,3S2,2S3成等差数列,
∴6S2=4S1+2S3,
即6(a1+a2)=4a1+2(a1+a2+a3),
则:a3=2a2,q=2,
∴${a}_{n}={2}^{n}$;
(Ⅱ)当n=1,2时,T1=6,T2=10,
当n≥3,Tn=10+1×23+3×24+…+(2n-5)•2n,
2Tn=20+1×24+3×25+…+(2n-7)×2n+(2n-5)×2n+1,
两式相减得:-Tn=-10+8+2(24+25+…+2n)-(2n-5)×2n+1,
=-2+2×$\frac{{2}^{4}(1-{2}^{n-3})}{1-2}$-(2n-5)×2n+1,
=-34+(7-2n)•2n+1,
∴Tn=34-(7-2n)•2n+1.
∴${T}_{n}=\left\{\begin{array}{l}{6}&{n=1}\\{10}&{n=2}\\{34-(7-2n)•{2}^{n+1}}&{n≥3}\end{array}\right.$.
点评 本题求等比数列的通项公式和采用错位相减法求前n项和,属于中档题.

练习册系列答案
相关题目
18.将函敬y=sin2x的图象向右平移$\frac{π}{4}$个单位长度,所得图象对应的函数解析式是( )
| A. | y=cos2x | B. | y=-cos2x | C. | y=sin(2x-$\frac{π}{4}$) | D. | y=-sin2x |
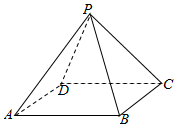 如图,正四棱锥P-ABCD的底面一边AB长为$2\sqrt{3}cm$,侧面积为$8\sqrt{3}c{m^2}$,则它的体积为4.
如图,正四棱锥P-ABCD的底面一边AB长为$2\sqrt{3}cm$,侧面积为$8\sqrt{3}c{m^2}$,则它的体积为4.