题目内容
10.已知函数f(x)=-x+log2$\frac{1-x}{1+x}$,若方程m-e-x=f(x)在[-$\frac{1}{3}$,$\frac{1}{3}$]内有实数解,则实数m的最小值是( )| A. | e${\;}^{-\frac{1}{3}}$+$\frac{4}{3}$ | B. | e${\;}^{\frac{1}{3}}$+$\frac{4}{3}$ | C. | e${\;}^{\frac{1}{3}}$-$\frac{4}{3}$ | D. | e${\;}^{-\frac{1}{3}}$-$\frac{4}{3}$ |
分析 化简f(x)=-x+log2$\frac{1-x}{1+x}$=-x+log2($\frac{2}{1+x}$-1),从而由复合函数及函数的四则运算可得函数f(x)是[-$\frac{1}{3}$,$\frac{1}{3}$]上的减函数;化简可得方程m=e-x+f(x)在[-$\frac{1}{3}$,$\frac{1}{3}$]内有实数解,而函数y=e-x+f(x)=e-x-x+log2$\frac{1-x}{1+x}$在[-$\frac{1}{3}$,$\frac{1}{3}$]上是减函数,从而可得实数m的最小值是${e}^{-\frac{1}{3}}$-$\frac{1}{3}$+log2$\frac{1}{2}$=${e}^{-\frac{1}{3}}$-$\frac{4}{3}$.
解答 解:∵f(x)=-x+log2$\frac{1-x}{1+x}$=-x+log2($\frac{2}{1+x}$-1),
而y=-x是[-$\frac{1}{3}$,$\frac{1}{3}$]上的减函数,y=$\frac{2}{1+x}$-1是[-$\frac{1}{3}$,$\frac{1}{3}$]上的减函数,y=log2x是(0,+∞)上的增函数,
∴函数f(x)是[-$\frac{1}{3}$,$\frac{1}{3}$]上的减函数;
∵方程m-e-x=f(x)在[-$\frac{1}{3}$,$\frac{1}{3}$]内有实数解,
∴方程m=e-x+f(x)在[-$\frac{1}{3}$,$\frac{1}{3}$]内有实数解,
又∵y=e-x在[-$\frac{1}{3}$,$\frac{1}{3}$]上是减函数,
∴函数y=e-x+f(x)=e-x-x+log2$\frac{1-x}{1+x}$在[-$\frac{1}{3}$,$\frac{1}{3}$]上是减函数,
∴${e}^{-\frac{1}{3}}$-$\frac{1}{3}$+log2$\frac{1}{2}$≤e-x-x+log2$\frac{1-x}{1+x}$≤${e}^{\frac{1}{3}}$+$\frac{1}{3}$+log22,
∴${e}^{-\frac{1}{3}}$-$\frac{1}{3}$+log2$\frac{1}{2}$≤m≤${e}^{\frac{1}{3}}$+$\frac{1}{3}$+log22,
∴实数m的最小值是${e}^{-\frac{1}{3}}$-$\frac{1}{3}$+log2$\frac{1}{2}$=${e}^{-\frac{1}{3}}$-$\frac{4}{3}$;
故选D.
点评 本题考查了函数的单调性的判断,复合函数与函数的四则运算的应用,同时考查了转化法的应用,属于中档题.

 小学课时特训系列答案
小学课时特训系列答案| A. | y=cos2x | B. | y=-cos2x | C. | y=sin(2x-$\frac{π}{4}$) | D. | y=-sin2x |
| A. | [-$\frac{1}{e}$,e) | B. | (-$\frac{1}{e}$,e) | C. | (-$\frac{1}{e}$,$\frac{1}{e}$) | D. | (0,e) |
| A. | a<1 | B. | a≤1 | C. | a≥0 | D. | a≤0 |
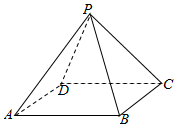 如图,正四棱锥P-ABCD的底面一边AB长为$2\sqrt{3}cm$,侧面积为$8\sqrt{3}c{m^2}$,则它的体积为4.
如图,正四棱锥P-ABCD的底面一边AB长为$2\sqrt{3}cm$,侧面积为$8\sqrt{3}c{m^2}$,则它的体积为4.