题目内容
9．若X～N（μ，σ2），a为一个实数，证明P（X=a）=0．分析 由分布函数定义，利用反证法，即可证明．
解答 证明：首先，P（X=a）≥0，
假设P（X=a）＞0，记P（X=a）=c，记X的分布函数为F（x），
则由分布函数定义，F（a+0）-F（a-0）=c＞0，由此知a是F（x）的间断点，这与F（x）在R上连续矛盾．
因此假设不成立，P（X=a）=0．
点评 本题考查分布函数定义，考查反证法，比较基础．
练习册系列答案
相关题目
18．将函敬y=sin2x的图象向右平移$\frac{π}{4}$个单位长度，所得图象对应的函数解析式是（ ）
| A． | y=cos2x | B． | y=-cos2x | C． | y=sin（2x-$\frac{π}{4}$） | D． | y=-sin2x |
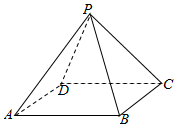如图，正四棱锥P-ABCD的底面一边AB长为$2\sqrt{3}cm$，侧面积为$8\sqrt{3}c{m^2}$，则它的体积为4．