题目内容
18. 有一个可同时进出水的容器,每单位时间内的水量是一定的,设从某时刻开始10min内只进水不出水,在随后的30min内既进水又出水,得到时间x(min)与水量y(L)之间的关系如图所示.若40min后只放水不进水,求y与x的函数关系.
有一个可同时进出水的容器,每单位时间内的水量是一定的,设从某时刻开始10min内只进水不出水,在随后的30min内既进水又出水,得到时间x(min)与水量y(L)之间的关系如图所示.若40min后只放水不进水,求y与x的函数关系.
分析 根据一次函数解析式得出求解,进水速度为每分钟;2(L),出水速度为每分钟;$\frac{5}{3}$(L),运用点(0,0).(10,20,)(40,30),利用斜率求解即可.
解答 解:∵0≤x≤10,0≤y≤20,过点(0,0),(10,20)
∴斜率为$\frac{20-0}{10-0}$=2,①②③
利用点斜式得出:y=2x,
∵10≤x≤40,20≤y≤30,
∴斜率为$\frac{30-20}{40-10}$=$\frac{1}{3}$,过点(10,20),(40,30)
∴y=$\frac{1}{3}x$$+\frac{50}{3}$
∴进水速度为每分钟;2(L),出水速度为每分钟;$\frac{5}{3}$(L),
运用点(0,0).(10,20,)(40,30)
根据函数y=kx+b求解得出
∴y=$\left\{\begin{array}{l}{2x,0≤x≤10}\\{\frac{1}{3}x+\frac{50}{3},10<x≤40}\\{-\frac{5x}{3}+\frac{290}{3},40<x≤58}\end{array}\right.$
点评 本题考察了一次函数性质,运用图形解决实际问题的能力,关键是利用数形结合的思想求解问题.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目
7.已知集合A={x|2x≤1,x∈R},B={a,1},若A∩B≠∅,则实数a的取值范围是( )
| A. | a<1 | B. | a≤1 | C. | a≥0 | D. | a≤0 |
8.“函数f(x)=x3+(a2-1)x2为奇函数”是“a=1”的( )
| A. | 必要不充分条件 | B. | 充分不必要条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
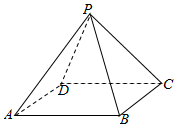 如图,正四棱锥P-ABCD的底面一边AB长为$2\sqrt{3}cm$,侧面积为$8\sqrt{3}c{m^2}$,则它的体积为4.
如图,正四棱锥P-ABCD的底面一边AB长为$2\sqrt{3}cm$,侧面积为$8\sqrt{3}c{m^2}$,则它的体积为4.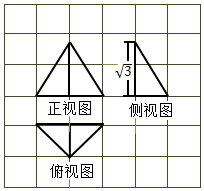 网格纸的各小格都是边长为1的正方形,图中粗实线画出的是一个几何体的三视图,其中正视图是正三角形,则该几何体的外接球表面积为$\frac{16π}{3}$.
网格纸的各小格都是边长为1的正方形,图中粗实线画出的是一个几何体的三视图,其中正视图是正三角形,则该几何体的外接球表面积为$\frac{16π}{3}$.