题目内容
1.已知数列{an}的前n项和为Sn,a1=0,4Sn=1-an+1,n∈N*.(1)求数列{an}的通项公式;
(2)记bn=(-1)nlog3a2n,求数列{bn}的前n项和Tn.
分析 (1)通过4Sn=1-an+1与4Sn-1=1-an作差,整理可知an+1=-3an,验证当n=1时是否成立即可;
(2)通过(1)可知bn=(-1)n2(n-1),进而分n为奇数、偶数两种情况讨论即可.
解答 解:(1)∵4Sn=1-an+1,
∴当n≥2时,4Sn-1=1-an,
两式相减得:4an=an-an+1,即an+1=-3an,
又∵a1=0,4Sn=1-an+1,
∴a2=1-4a1=1不满足上式,
∴an=$\left\{\begin{array}{l}{0,}&{n=1}\\{(-3)^{n-2},}&{n≥2}\end{array}\right.$;
(2)由(1)可知a2n=(-3)2n-2=32n-2,
∴bn=(-1)nlog3a2n=(-1)nlog332n-2=(-1)n2(n-1),
当n为奇数时,Tn=0+2-4+6+…-2(n-3)+2(n-2)-2(n-1)
=$\frac{n-1}{2}$×2-2(n-1)
=-n+1;
当n为偶数时,Tn=0+2-4+6+…+2(n-3)-2(n-2)+2(n-1)=$\frac{n}{2}$×2=n;
综上所述,数列{bn}的前n项和Tn=$\left\{\begin{array}{l}{-n+1,}&{n为奇数}\\{n,}&{n为偶数}\end{array}\right.$.
点评 本题考查数列的通项及前n项和,考查分类讨论的思想,注意解题方法的积累,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.知函数f(x)=ex-ax的图象在区间(-1,+∞)内与x轴没有交点,则实数a的取值范围是( )
| A. | [-$\frac{1}{e}$,e) | B. | (-$\frac{1}{e}$,e) | C. | (-$\frac{1}{e}$,$\frac{1}{e}$) | D. | (0,e) |
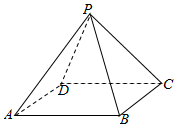 如图,正四棱锥P-ABCD的底面一边AB长为$2\sqrt{3}cm$,侧面积为$8\sqrt{3}c{m^2}$,则它的体积为4.
如图,正四棱锥P-ABCD的底面一边AB长为$2\sqrt{3}cm$,侧面积为$8\sqrt{3}c{m^2}$,则它的体积为4.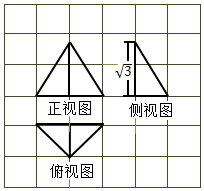 网格纸的各小格都是边长为1的正方形,图中粗实线画出的是一个几何体的三视图,其中正视图是正三角形,则该几何体的外接球表面积为$\frac{16π}{3}$.
网格纸的各小格都是边长为1的正方形,图中粗实线画出的是一个几何体的三视图,其中正视图是正三角形,则该几何体的外接球表面积为$\frac{16π}{3}$.