题目内容

1．已知函数f（x）=x2-2kx+8在区间[5，20]上具有单调性，则实数k的取值范围是（-∞，5]∪[20，+∞）．

分析 令对称轴不在区间[5，20]上即可．

解答 解：f（x）的对称轴为x=k，∵f（x）=x2-2kx+8在区间[5，20]上具有单调性，∴k≤5或k≥20．
故答案为（-∞，5]∪[20，+∞）．

点评 本题考查了二次函数的单调性与对称轴的关系，属于基础题．

练习册系列答案
相关题目
11．已知幂函数f（x）的图象过点（4，$\frac{1}{2}$），则f（8）的值为（　　）
A．$\frac{\sqrt{2}}{4}$B．64C．2$\sqrt{2}$D．$\frac{1}{64}$
12．在△ABC中，内角A，B，C的对边分别为a，b，c，已知a=2$\sqrt{3}$，b=2$\sqrt{2}$，B=45°，则A等于（　　）
A．30°或150°B．60°C．60°或120°D．30°
9．函数f（x）=log2x-$\frac{1}{2}$x+5的零点个数为（　　）
A．0B．1C．3D．2
16．下列图象是函数y=$\left\{\begin{array}{l}{x^2}，x＜0\\ x-1，x≥0\end{array}$的图象的是（　　）
A．B．C．D．
6．函数f（x）是定义在R上的奇函数，并且当x∈（0，+∞）时，f（x）=lgx2，那么，f（-10）=（　　）
A．-1B．-2C．2D．10
13．给出下列说法：
①集合A={x∈Z|x=2k-1，k∈Z}与集合B={x∈Z|x=2k+1，k∈Z}是相等集合；
②若函数f（x）的定义域为[0，2]，则函数f（2x）的定义域为[0，4]；
③定义在R上的函数f（x）对任意两个不等实数a、b，总有$\frac{f（a）-f（b）}{a-b}$＞0成立，则f（x）在R上是增函数；
④存在实数m，使f（x）=x2+mx+1为奇函数．
正确的有①③．
10．设x3+ax+b=0，其中a，b均为实数，给出下列条件中，①a=-3，b=-3；②a=-3，b=2；③a=0，b=2．其中能使得该三次方程仅有一个实根的是（　　）
A．①②B．①③C．②③D．①②③
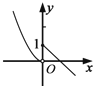
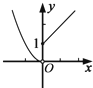
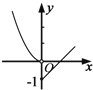
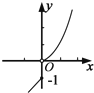
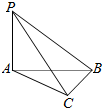13．如图，Rt△ABC中，∠ACB=90°，∠BAC=45°，PA⊥平面ABC，且PA=BC=1，则二面角A-PB-C的平面角是60°．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网